Ambos o NumPy e o Pandas têm o conceito de eixo (ou axis em inglês), mas eles são usados de maneiras ligeiramente diferentes.
No NumPy, o eixo refere-se à dimensão ao longo da qual uma determinada operação é realizada. Já no Pandas, o parâmetro axis tem um significado ligeiramente diferente, referindo-se à direção ao longo da qual uma operação deve ser realizada.
Neste artigo, veremos exemplos e consequências deste conceito em cada biblioteca.
NumPy #
Como escrito no início do artigo, no NumPy o eixo refere-se à dimensão ao longo
da qual uma determinada operação é realizada. Por exemplo, ao calcular a soma de
uma matriz NumPy, você pode especificar o eixo ao longo do qual a soma deve ser
calculada. Se a matriz tiver a forma (3, 4), então o parâmetro de eixo pode ser
definido como 0 ou 1. Se axis=0, a soma é calculada ao longo da primeira
dimensão, resultando em um array 1D de comprimento 4. Se axis=1, a soma é
calculada ao longo da segunda dimensão, resultando em um array 1D de comprimento
3.
Veremos este exemplo com duas dimensões, e depois vamos expandir para exemplos mais complexos, com mais dimensões.
Duas dimensões #
Comecemos importando a biblioteca e criando um array bidimensional, conferindo o
comprimento de suas dimensões com o atributo shape. Caso tenha dúvidas sobre
os conceitos de dimensão e shape (forma) no contexto do NumPy, veja este
artigo.
import numpy as np
arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
arr
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
arr.shape
(3, 4)
Como explicado anteriormente, o axis define em qual dimensão determinada operação será feita. Logo, façamos uma soma dos valores ao longo da primeira dimensão:
sum_axis_0 = np.sum(arr, axis=0)
sum_axis_0
array([15, 18, 21, 24])
Obtivemos 4 valores em um array unidimensional. Cada um deles é a soma dos
valores ao longo da dimensão de tamanho 3. Como o array original arr é
bidimensional, você pode visualizar mais facilmente se imaginar que os valores
são as somas de cada coluna de uma matriz bidimensional. Mas não se apegue muito
a esta visualização, pois ela não será muito útil quando aumentarmos a
quantidade de dimensões.
Vejamos a soma ao longo da segunda dimensão:
sum_axis_1 = np.sum(arr, axis=1)
sum_axis_1
array([10, 26, 42])
Aqui, temos um array unidimensional de 3 valores. Cada um deles é a soma dos valores ao longo da dimensão de tamanho 4. Seguindo nossa analogia visual, você pode enxergar como sendo a soma de cada linha de nossa matriz bidimensional.
É importante notar que o parâmetro de eixo pode ser usado com muitos outros métodos NumPy, não apenas com a soma. Por exemplo, ao calcular a média, a mediana ou o desvio padrão de uma matriz, o parâmetro de eixo pode ser usado para especificar ao longo de qual dimensão o cálculo deve ser feito. Isso é especialmente útil quando se trabalha com matrizes de alta dimensão, onde as operações podem se tornar complexas. Daí o parâmetro de eixo ser uma das principais ferramentas que os cientistas de dados usam para manipular e transformar dados em matrizes NumPy.
As operações de slice continuam sendo válidas, de forma que também podemos realizar operações em partes de nossa matriz, indicando o eixo desejado:
# Somando as duas primeiras linhas ao longo do eixo 0
sum_rows = np.sum(arr[:2, :], axis=0)
sum_rows
array([ 6, 8, 10, 12])
# Somando todas as linhas das primeira e terceira colunas ao longo do eixo 0
sum_cols = np.sum(arr[:, [0, 2]], axis=0)
sum_cols
array([15, 21])
Três dimensões #
Para três dimensões, a linha de raciocínio é a mesma, mas a analogia de linhas e colunas que usamos acima pode não ajudar muito. Aqui utilizaremos recursos visuais para efetivamente compreender a ideia de eixo de uma operação. Primeiro, criemos um array 3D com inteiros aleatórios:
# Definindo uma seed fixa, de forma que seja possível reproduzir o artigo igualmente
rng = np.random.default_rng(seed=42)
# Criando um array 3D com valores inteiros aleatórios de 0 a 9
arr_3d = rng.integers(low=0, high=9, size=(2, 3, 4), endpoint=True)
Conferindo o shape:
arr_3d.shape
(2, 3, 4)
Vejamos como o NumPy nos apresenta tal array:
arr_3d
array([[[0, 7, 6, 4],
[4, 8, 0, 6],
[2, 0, 5, 9]],
[[7, 7, 7, 7],
[5, 1, 8, 4],
[5, 3, 1, 9]]])
Observe que ele apresenta como se fossem dois conjuntos de dados. Inclusive,
podemos pegar cada conjunto e verificar seu shape:
arr_3d[0]
array([[0, 7, 6, 4],
[4, 8, 0, 6],
[2, 0, 5, 9]])
arr_3d[0].shape
(3, 4)
arr_3d[1]
array([[7, 7, 7, 7],
[5, 1, 8, 4],
[5, 3, 1, 9]])
arr_3d[1].shape
(3, 4)
Ou seja, temos duas matrizes bidimensionais com 3 linhas e 4 colunas, arranjadas ao longo de uma dimensão de comprimento 2. Confuso? Veja a seguinte imagem:
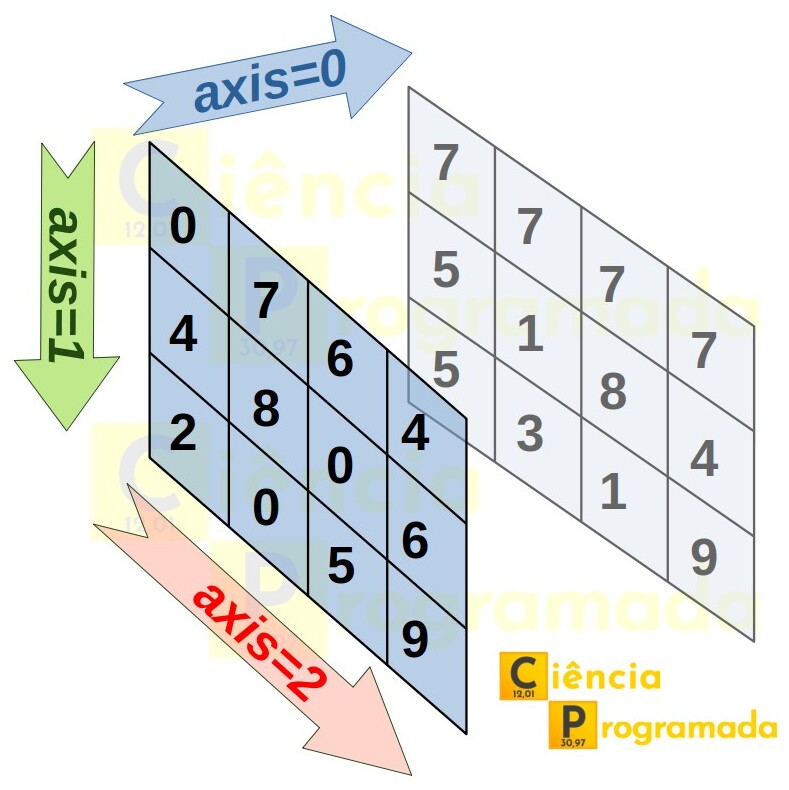
Com auxílio da imagem, o que acontece, então, se solicitamos a soma ao longo do
eixo 0? Ora, é como se estivéssemos empurrando a matriz da frente contra a
matriz de trás. Logo, deve ser a soma item a item de uma matriz com a outra, e o
shape resultante deve ser igual ao shape da matriz resultante:
sum_axis_0 = arr_3d.sum(axis=0)
display(sum_axis_0)
display(sum_axis_0.shape)
array([[ 7, 14, 13, 11],
[ 9, 9, 8, 10],
[ 7, 3, 6, 18]])
(3, 4)
Confira o resultado e veja que é realmente o que foi descrito. E aqui já temos
uma primeira dica que é muito útil quando analisamos resultados de dimensões
muito elevadas, de difícil visualização: o shape resultante é igual ao
original retirando-se a dimensão na qual se está aplicando a operação. No caso,
nosso array original tem shape (2, 3, 4), estamos realizando a operação de soma
ao longo da dimensão de comprimento 2, de forma que o shape resultante exclui
esta dimensão, ficando (3, 4). Guarde esta dica para analisar os exemplos
seguintes.
No caso específico desta soma que fizemos, o resultado é o mesmo de adicionar
explicitamente cada matriz bidimensional presente em cada posição do primeiro
eixo (axis=0):
arr_3d[0] + arr_3d[1]
array([[ 7, 14, 13, 11],
[ 9, 9, 8, 10],
[ 7, 3, 6, 18]])
Mas, claro, é mais eficiente e sucinto utilizar a notação de eixo.
Modifiquemos agora nosso exemplo, solicitando a soma ao longo do eixo 1:
sum_axis_1 = arr_3d.sum(axis=1)
display(sum_axis_1)
display(sum_axis_1.shape)
array([[ 6, 15, 11, 19],
[17, 11, 16, 20]])
(2, 4)
Veja que o shape é o esperado conforme a dica que passamos anteriormente. Como
estamos olhando segunda dimensão, de comprimento 3, o shape resultante é dado
pelos comprimentos das demais dimensões, sendo (2, 4).
Os valores nada mais são que as somas ao longo do eixo 1, que pode ser entendido como as somas de cada coluna de cada matriz bidimensional, conforme a figura apresentada. Como são duas matrizes, cada uma com quatro colunas, temos como resultado uma matriz bidimensional 2 x 4.
Perceba como a sintaxe do NumPy facilita muito esta operação. Além de a realizar eficientemente quanto a memória e velocidade de execução. Se fossemos realizar tal soma manualmente, a partir de uma função própria, precisaríamos iterar por cada matriz de nosso array tridimensional e, em cada matriz, iterar por cada coluna armazenando as somas de cada uma. Apenas a título de exercício, podemos criar tal função e realizar a soma ao longo do eixo 1:
def sum_column(matrix):
result = []
for column in range(len(matrix[0])):
total = 0
for row in matrix:
total += row[column]
result.append(total)
return result
sum_axis_1_function = []
for matrix in arr_3d:
sum_axis_1_function.append(sum_column(matrix))
np.array(sum_axis_1_function)
array([[ 6, 15, 11, 19],
[17, 11, 16, 20]])
O resultado é o mesmo obtido pelo NumPy, mas o código é certamente mais difícil de manter e ineficiente do ponto de vista de memória e velocidade. Esta é a beleza do NumPy e suas operações vetorizadas. Ou seja, ele é otimizado para aplicar algoritmos usualmente elaborados para operações elemento a elemento, como nossa função acima, em conjuntos de valores. O ganho de performance e semântica é significativo.
Ainda temos mais uma dimensão em nosso array. Seguindo a mesma lógica, sabemos que o array resultante da operação de soma ao longo desse eixo terá seu shape (2, 3), pois estamos olhando a dimensão de comprimento 4 de nosso array original. E, pela figura, pode ser entendido como as somas de cada linha de cada matriz bidimensional. Como são duas matrizes, cada uma com três linhas, temos como resultado uma matriz bidimensional 2 x 3. Conferindo:
sum_axis_2 = arr_3d.sum(axis=2)
display(sum_axis_2)
display(sum_axis_2.shape)
array([[17, 18, 16],
[28, 18, 18]])
(2, 3)
Assim como feito anteriormente, apenas para fins didáticos, podemos verificar que este é exatamente o mesmo resultado que seria obtido criando uma função para iterar por cada linha de cada matriz realizando a soma:
def sum_row(matrix):
result = []
for row in matrix:
total = sum(row)
result.append(total)
return result
sum_axis_2_function = []
for matrix in arr_3d:
sum_axis_2_function.append(sum_row(matrix))
np.array(sum_axis_2_function)
array([[17, 18, 16],
[28, 18, 18]])
Novamente, é muito mais eficiente utilizar as operações vetorizadas do NumPy. Mas deixo as funções neste artigo para facilitar a compreensão e visualização dos resultados obtidos.
Mais de três dimensões #
Até 3 dimensões, figuras e esquemas nos ajudam a ter uma ideia visual. No entanto, o grande poder do NumPy é possibilitar trabalhar em problemas que, conceitualmente, podem envolver múltiplas dimensões. Se a lógica apresentada até aqui foi compreendida por você, os resultados para dimensões superiores serão bastante naturais, mesmo que nossa capacidade de visualização seja prejudicada pela nossa limitação visual a três dimensões.
Geremos um array de números inteiros de 4 dimensões:
arr_4d = rng.integers(low=0, high=9, size=(2, 2, 3, 4), endpoint=True)
arr_4d
array([[[[7, 6, 4, 8],
[5, 4, 4, 2],
[0, 5, 8, 0]],
[[8, 8, 2, 6],
[1, 7, 7, 3],
[0, 9, 4, 8]]],
[[[6, 7, 7, 1],
[3, 4, 4, 0],
[5, 1, 7, 6]],
[[9, 7, 3, 9],
[4, 3, 9, 3],
[0, 4, 7, 1]]]])
Veja que geramos um array de shape (2, 2, 3, 4). Ora, isto significa que temos a primeira dimensão com comprimento 2, cada posição desta dimensão armazenando um array tridimensional de forma (2, 3, 4). Não por acaso, vemos na maneira que o NumPy apresenta o array dois conjuntos claros de arrays. E, dentro de cada um destes, outros dois conjuntos que podemos visualizar como arrays bidimensionais de forma (3, 4). Tudo que descrevemos neste parágrafo segue a mesma linha de raciocínio que adotamos em 3 dimensões, apenas expandimos para uma dimensão adicional.
Podemos visualizar cada posição da primeira dimensão de nosso array quadridimensional:
arr_4d[0]
array([[[7, 6, 4, 8],
[5, 4, 4, 2],
[0, 5, 8, 0]],
[[8, 8, 2, 6],
[1, 7, 7, 3],
[0, 9, 4, 8]]])
arr_4d[1]
array([[[6, 7, 7, 1],
[3, 4, 4, 0],
[5, 1, 7, 6]],
[[9, 7, 3, 9],
[4, 3, 9, 3],
[0, 4, 7, 1]]])
Agora, façamos a soma ao longo dessa dimensão, ao longo de axis=0:
sum_axis_0_4d = arr_4d.sum(axis=0)
display(sum_axis_0_4d)
display(sum_axis_0_4d.shape)
array([[[13, 13, 11, 9],
[ 8, 8, 8, 2],
[ 5, 6, 15, 6]],
[[17, 15, 5, 15],
[ 5, 10, 16, 6],
[ 0, 13, 11, 9]]])
(2, 3, 4)
O shape é o resultado que esperamos seguindo a dica dada mais acima no artigo e a discussão feita anteriormente. E os valores são o resultado de somar, item a item, os arrays 3D presentes no eixo.
Para axis=1 temos:
display(arr_4d.sum(axis=1))
display(arr_4d.sum(axis=1).shape)
array([[[15, 14, 6, 14],
[ 6, 11, 11, 5],
[ 0, 14, 12, 8]],
[[15, 14, 10, 10],
[ 7, 7, 13, 3],
[ 5, 5, 14, 7]]])
(2, 3, 4)
Aqui é a dimensão onde entramos no array 3D presente em cada posição do eixo 0. Assim, estamos somando item a item as matrizes bidimensionais em cada array 3D.
Para axis=2:
display(arr_4d.sum(axis=2))
display(arr_4d.sum(axis=2).shape)
array([[[12, 15, 16, 10],
[ 9, 24, 13, 17]],
[[14, 12, 18, 7],
[13, 14, 19, 13]]])
(2, 2, 4)
Seguindo a lógica, é a soma de cada coluna (são 4 colunas) dentro de cada matriz bidimensional, dentro de cada array 3D (são 2 arrays), dentro de cada posição de nosso array 4D (são 2 posições).
Por fim, para axis=3:
display(arr_4d.sum(axis=3))
display(arr_4d.sum(axis=3).shape)
array([[[25, 15, 13],
[24, 18, 21]],
[[21, 11, 19],
[28, 19, 12]]])
(2, 2, 3)
Analogamente, é a soma de cada linha (são 3 linhas) dentro de cada matriz bidimensional, dentro de cada array 3D (são 2 arrays), dentro de cada posição de nosso array 4D (são 2 posições).
Se tiver dificuldade, leia novamente, faça contas em um pedaço de papel, ou faça esquemas. Eu mesmo fiz isto para entender quando tive contato com estas operações. Mas uma vez entendido, nunca mais você terá dificuldade em entender o resultado de uma operação envolvendo eixos no NumPy!
Pandas #
Já escrevemos aqui no site sobre como as estruturas básicas do Pandas, Series e DataFrames, são construídas sobre os arrays do NumPy. No entanto, os dataframes do Pandas são, por definição, feitos para serem similares a estruturas tabulares, bidimensionais, com colunas e linhas. Desta forma, precisamos entender como o conceito de eixo deve ser entendido nesta biblioteca.
DataFrames simples #
Acredito que o exemplo mais simples seja transformar nosso array bidimensional que serviu de primeiro exemplo do NumPy em um dataframe do Pandas. Lembrando, o array era:
arr
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
Transformado em dataframe:
import pandas as pd
arr_to_df = pd.DataFrame(arr)
arr_to_df
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 |
| 1 | 5 | 6 | 7 | 8 |
| 2 | 9 | 10 | 11 | 12 |
Vejamos como será o resultado de solicitar a soma ao longo de axis=0:
arr_to_df.sum(axis=0, numeric_only=True)
0 15
1 18
2 21
3 24
dtype: int64
Ora, nada mais temos que o resultado da soma de cada coluna. E os valores são os
mesmos que obtivemos, na forma de array, quando fizemos a soma ao longo de
axis=0 no array original do NumPy.
Analogamente, para axis=1:
arr_to_df.sum(axis=1, numeric_only=True)
0 10
1 26
2 42
dtype: int64
Temos que o resultado da soma de cada linha. E os valores são os mesmos que
obtivemos, na forma de array, quando realizamos a soma ao longo de axis=1 no
array original do NumPy.
Mas, se os resultados são os mesmos, há, então, alguma diferença?
Neste caso específico, não. Mas vamos considerar um exemplo mais usual de dataframe que irá ajudar a perceber algumas particularidades da biblioteca e servirá de modelo básico para as próximas discussões.
Como dito no início desta seção, o Pandas foi pensado para lidar com dados tabulares. Isto significa que as colunas representam as variáveis, cada uma com um nome exclusivo e com um tipo de dado específico, e as linhas representam as observações ou registros no conjunto de dados. Considere o dataframe a seguir, com nome, idade e salário para três pessoas fictícias:
data = {
"Nome": ["Alice", "Bruno", "Carlos"],
"Idade": [25, 30, 35],
"Salário": [50000, 60000, 70000],
}
df = pd.DataFrame(data)
df
| Nome | Idade | Salário | |
|---|---|---|---|
| 0 | Alice | 25 | 50000 |
| 1 | Bruno | 30 | 60000 |
| 2 | Carlos | 35 | 70000 |
Agora temos mais significado para nossos dados. Fica bem claro que, se quisermos
a média de idade e de salário das pessoas, estamos olhando para as colunas, o
que significa axis=0 no Pandas:
mean_axis_0 = df.mean(axis=0, numeric_only=True)
mean_axis_0
Idade 30.0
Salário 60000.0
dtype: float64
Como a biblioteca espera sempre um formato tabular, onde cada coluna tem
diversos registros de um mesmo tipo, o parâmetro axis=0 costuma ser o padrão
nos métodos do Pandas. Desta forma, seria suficiente:
df.mean(numeric_only=True)
Idade 30.0
Salário 60000.0
dtype: float64
Os mais habituados com a biblioteca provavelmente têm o costume de aplicar um filtro selecionando a(s) coluna(s) desejada(s). Assim, poderíamos calcular a média apenas para a coluna Idade, por exemplo:
df["Idade"].mean()
30.0
Desta forma, fica explícito que a operação está atuando sobre uma coluna. Também poderíamos fazer como abaixo, para as duas colunas:
df[["Idade", "Salário"]].mean()
Idade 30.0
Salário 60000.0
dtype: float64
Evidentemente, poderíamos solicitar a média por linha com axis=1:
mean_axis_1 = df.mean(axis=1, numeric_only=True)
mean_axis_1
0 25012.5
1 30015.0
2 35017.5
dtype: float64
Mas qual seria o significado destes valores? Não consigo enxergar nenhum. Claro que podem haver contextos onde aplicar operações em linhas façam sentido, veremos alguns a seguir, mas a ideia é mostrar que, como o Pandas trabalha com a ideia de dados tabulares, as operações são pensadas primariamente para aplicação em colunas. Da mesma forma que lidamos com planilhas em programas como o Excel.
Pelo discutido, talvez o leitor já tenha inferido que não faz sentido axis=2
ou valores superiores no Pandas. Afinal, se sempre somos reduzidos a dados
tabulares, teremos ou colunas (axis=0), ou linhas (axis=1). Porém, isto não
significa que não podemos ter mais dimensões, só precisamos entender o que elas
significam no contexto da biblioteca.
Dataframes com MultiIndex #
Assim como na seção anterior transformamos nosso array bidimensional estudado com o NumPy em um dataframe, façamos o mesmo agora com nosso array tridimensional. A questão é como passar a ideia das dimensões. Para isso podemos trabalhar com dataframes com múltiplos índices.
index = pd.MultiIndex.from_product(
[range(s) for s in arr_3d.shape], names=["dim1", "dim2", "dim3"]
)
df_multi = pd.DataFrame(
{"dados": arr_3d.flatten()},
index=index,
)
df_multi
| dados | |||
|---|---|---|---|
| dim1 | dim2 | dim3 | |
| 0 | 0 | 0 | 0 |
| 1 | 7 | ||
| 2 | 6 | ||
| 3 | 4 | ||
| 1 | 0 | 4 | |
| 1 | 8 | ||
| 2 | 0 | ||
| 3 | 6 | ||
| 2 | 0 | 2 | |
| 1 | 0 | ||
| 2 | 5 | ||
| 3 | 9 | ||
| 1 | 0 | 0 | 7 |
| 1 | 7 | ||
| 2 | 7 | ||
| 3 | 7 | ||
| 1 | 0 | 5 | |
| 1 | 1 | ||
| 2 | 8 | ||
| 3 | 4 | ||
| 2 | 0 | 5 | |
| 1 | 3 | ||
| 2 | 1 | ||
| 3 | 9 |
Vamos entender o que fizemos acima. Os valores de nosso array foram listados na
coluna dados, mas foram hierarquizados em níveis com auxílio dos índices
dim1, dim2, dim3. Veja como os índices criam a ideia de níveis, grupos,
categorias, ou hierarquia dentro de nosso dataframe. Você verá estas palavras
que listei com frequência no estudo de dataframes com múltiplos índices.
Perceba, também, que, embora estejamos numa estrutura bidimensional, os índices
agregam dimensões semânticas aos nossos dados. Isto ficará mais evidente nos
próximos exemplos mas, antes, vejamos algumas consequências.
Como dito, os índices criam uma ideia de grupos em níveis. Assim, podemos usar o
método groupby e agrupar por um determinado nível. E, com os dados agrupados,
passar alguma função como, por exemplo, sum para somar os dados de um
determinado nível:
df_multi.groupby(level="dim1").sum()
| dados | |
|---|---|
| dim1 | |
| 0 | 51 |
| 1 | 64 |
df_multi.groupby(level="dim2").sum()
| dados | |
|---|---|
| dim2 | |
| 0 | 45 |
| 1 | 36 |
| 2 | 34 |
E nada impede que sejam passados mais de um nível:
df_multi.groupby(level=["dim1", "dim2"]).sum()
| dados | ||
|---|---|---|
| dim1 | dim2 | |
| 0 | 0 | 17 |
| 1 | 18 | |
| 2 | 16 | |
| 1 | 0 | 28 |
| 1 | 18 | |
| 2 | 18 |
Talvez este exemplo com índices de nomes genéricos dim1, dim2, e dim3
esteja abstrato demais para ficar claro o potencial do que estamos fazendo aqui.
Assim, vamos adicionar mais semântica ao exemplo, mantendo a base no nosso array
tridimensional:
dates = pd.date_range("2022-01", periods=arr_3d.shape[0], freq="M", name="Data")
stores = ["Loja1", "Loja2", "Loja3"]
products = ["ProdutoA", "ProdutoB", "ProdutoC", "ProdutoD"]
multi_index = pd.MultiIndex.from_product(
[dates, stores, products], names=["Data", "Loja", "Produto"]
)
df_vendas = pd.DataFrame({"Vendas": arr_3d.flatten()}, index=multi_index)
df_vendas
| Vendas | |||
|---|---|---|---|
| Data | Loja | Produto | |
| 2022-01-31 | Loja1 | ProdutoA | 0 |
| ProdutoB | 7 | ||
| ProdutoC | 6 | ||
| ProdutoD | 4 | ||
| Loja2 | ProdutoA | 4 | |
| ProdutoB | 8 | ||
| ProdutoC | 0 | ||
| ProdutoD | 6 | ||
| Loja3 | ProdutoA | 2 | |
| ProdutoB | 0 | ||
| ProdutoC | 5 | ||
| ProdutoD | 9 | ||
| 2022-02-28 | Loja1 | ProdutoA | 7 |
| ProdutoB | 7 | ||
| ProdutoC | 7 | ||
| ProdutoD | 7 | ||
| Loja2 | ProdutoA | 5 | |
| ProdutoB | 1 | ||
| ProdutoC | 8 | ||
| ProdutoD | 4 | ||
| Loja3 | ProdutoA | 5 | |
| ProdutoB | 3 | ||
| ProdutoC | 1 | ||
| ProdutoD | 9 |
Os valores são exatamente os mesmos de nosso dataframe anterior. No entanto, agora vemos que há níveis para nossos dados: produto a que se referem, lojas destes produtos, mês a que os valores se referem. E os valores representam o total de unidades vendidas de cada produto.
Os agrupamentos agora vão ter muito mais significado para nós. Agrupando por data e solicitando a soma, teremos o total de unidades vendidas por mês:
df_vendas.groupby(level="Data").sum()
| Vendas | |
|---|---|
| Data | |
| 2022-01-31 | 51 |
| 2022-02-28 | 64 |
Podemos detalhar por mês e por loja:
df_vendas.groupby(level=["Data", "Loja"]).sum()
| Vendas | ||
|---|---|---|
| Data | Loja | |
| 2022-01-31 | Loja1 | 17 |
| Loja2 | 18 | |
| Loja3 | 16 | |
| 2022-02-28 | Loja1 | 28 |
| Loja2 | 18 | |
| Loja3 | 18 |
Compare os resultados com o obtido na seção referente ao NumPy, quando a soma
foi feita ao longo de axis=2.
Também podemos detalhar por mês e produto:
df_vendas.groupby(level=["Data", "Produto"]).sum()
| Vendas | ||
|---|---|---|
| Data | Produto | |
| 2022-01-31 | ProdutoA | 6 |
| ProdutoB | 15 | |
| ProdutoC | 11 | |
| ProdutoD | 19 | |
| 2022-02-28 | ProdutoA | 17 |
| ProdutoB | 11 | |
| ProdutoC | 16 | |
| ProdutoD | 20 |
Compare os resultados com o obtido na seção referente ao NumPy, quando a soma
foi feita ao longo de axis=1.
Conseguiu entender as comparações? Obtivemos os mesmos resultados numéricos, mas agora com um significado atrelado, dados pelos índices do Pandas. São os índices que agregam mais dimensões ao dataframe, sendo dimensões do ponto de vista semântico, o dataframe continua sendo uma estrutura tabular de linhas e colunas.
Podemos fazer o mesmo com nosso array quadridimensional criado na seção de NumPy:
dates = pd.date_range("2022-01", periods=arr_4d.shape[0], freq="M", name="Data")
stores = ["Loja1", "Loja2", "Loja3"]
products = ["ProdutoA", "ProdutoB", "ProdutoC", "ProdutoD"]
multi_index = pd.MultiIndex.from_product(
[dates, stores, products], names=["Data", "Loja", "Produto"]
)
# Create a DataFrame from the 3D NumPy array and the MultiIndex
df_vendas_preco_unit = pd.DataFrame(
arr_4d.reshape(-1, 2),
index=multi_index,
columns=["UnidadesVendidas", "PrecoUnidade"],
)
# Print the DataFrame
df_vendas_preco_unit
| UnidadesVendidas | PrecoUnidade | |||
|---|---|---|---|---|
| Data | Loja | Produto | ||
| 2022-01-31 | Loja1 | ProdutoA | 7 | 6 |
| ProdutoB | 4 | 8 | ||
| ProdutoC | 5 | 4 | ||
| ProdutoD | 4 | 2 | ||
| Loja2 | ProdutoA | 0 | 5 | |
| ProdutoB | 8 | 0 | ||
| ProdutoC | 8 | 8 | ||
| ProdutoD | 2 | 6 | ||
| Loja3 | ProdutoA | 1 | 7 | |
| ProdutoB | 7 | 3 | ||
| ProdutoC | 0 | 9 | ||
| ProdutoD | 4 | 8 | ||
| 2022-02-28 | Loja1 | ProdutoA | 6 | 7 |
| ProdutoB | 7 | 1 | ||
| ProdutoC | 3 | 4 | ||
| ProdutoD | 4 | 0 | ||
| Loja2 | ProdutoA | 5 | 1 | |
| ProdutoB | 7 | 6 | ||
| ProdutoC | 9 | 7 | ||
| ProdutoD | 3 | 9 | ||
| Loja3 | ProdutoA | 4 | 3 | |
| ProdutoB | 9 | 3 | ||
| ProdutoC | 0 | 4 | ||
| ProdutoD | 7 | 1 |
Observe, agora, que temos duas colunas de valores. Uma indica a quantidade de unidades vendidas para cada produto, de cada loja, por cada mês. A outra, o preço de cada unidade de produto, para cada loja, a cada mês. Pense que é um relatório de uma média ou grande empresa, que possui lojas com os mesmos produtos, mas em regiões geográficas distintas. Assim, cada região pode ter preços distintos para um mesmo produto a depender das relações oferta/demanda oriundas da situação socioeconômica de cada região.
Neste contexto, faz sentido uma operação de multiplicação a cada linha, para
obter a receita de venda, que é a multiplicação da quantidade de unidades
vendidas pelo preço de cada unidade. O método prod nos possibilita realizar
esta operação facilmente:
df_vendas_preco_unit.prod(axis=1)
Data Loja Produto
2022-01-31 Loja1 ProdutoA 42
ProdutoB 32
ProdutoC 20
ProdutoD 8
Loja2 ProdutoA 0
ProdutoB 0
ProdutoC 64
ProdutoD 12
Loja3 ProdutoA 7
ProdutoB 21
ProdutoC 0
ProdutoD 32
2022-02-28 Loja1 ProdutoA 42
ProdutoB 7
ProdutoC 12
ProdutoD 0
Loja2 ProdutoA 5
ProdutoB 42
ProdutoC 63
ProdutoD 27
Loja3 ProdutoA 12
ProdutoB 27
ProdutoC 0
ProdutoD 7
dtype: int64
O retorno não é um dataframe, como podemos verificar com a função type:
type(_)
pandas.core.series.Series
O que obtivemos é uma série do Pandas. Podemos alocar esta série em uma coluna do nosso dataframe de início:
df_vendas_preco_unit["ReceitaTotal"] = df_vendas_preco_unit.prod(axis=1)
df_vendas_preco_unit
| UnidadesVendidas | PrecoUnidade | ReceitaTotal | |||
|---|---|---|---|---|---|
| Data | Loja | Produto | |||
| 2022-01-31 | Loja1 | ProdutoA | 7 | 6 | 42 |
| ProdutoB | 4 | 8 | 32 | ||
| ProdutoC | 5 | 4 | 20 | ||
| ProdutoD | 4 | 2 | 8 | ||
| Loja2 | ProdutoA | 0 | 5 | 0 | |
| ProdutoB | 8 | 0 | 0 | ||
| ProdutoC | 8 | 8 | 64 | ||
| ProdutoD | 2 | 6 | 12 | ||
| Loja3 | ProdutoA | 1 | 7 | 7 | |
| ProdutoB | 7 | 3 | 21 | ||
| ProdutoC | 0 | 9 | 0 | ||
| ProdutoD | 4 | 8 | 32 | ||
| 2022-02-28 | Loja1 | ProdutoA | 6 | 7 | 42 |
| ProdutoB | 7 | 1 | 7 | ||
| ProdutoC | 3 | 4 | 12 | ||
| ProdutoD | 4 | 0 | 0 | ||
| Loja2 | ProdutoA | 5 | 1 | 5 | |
| ProdutoB | 7 | 6 | 42 | ||
| ProdutoC | 9 | 7 | 63 | ||
| ProdutoD | 3 | 9 | 27 | ||
| Loja3 | ProdutoA | 4 | 3 | 12 | |
| ProdutoB | 9 | 3 | 27 | ||
| ProdutoC | 0 | 4 | 0 | ||
| ProdutoD | 7 | 1 | 7 |
Agora, temos em um coluna uma informação obtida por operações linha a linha. Estando em uma coluna, pode ser utilizada em agrupamentos. Por exemplo, total de unidades e de receita por mês:
df_vendas_preco_unit.groupby(level="Data")[["UnidadesVendidas", "ReceitaTotal"]].sum()
| UnidadesVendidas | ReceitaTotal | |
|---|---|---|
| Data | ||
| 2022-01-31 | 50 | 238 |
| 2022-02-28 | 64 | 244 |
Repare que não faz sentido incluir a coluna de preço de cada unidade, daí a seleção de colunas. O agrupamento também poderia ter sido feito por loja, considerando todo o período de tempo de nossa base de dados:
df_vendas_preco_unit.groupby(level="Loja")[["UnidadesVendidas", "ReceitaTotal"]].sum()
| UnidadesVendidas | ReceitaTotal | |
|---|---|---|
| Loja | ||
| Loja1 | 40 | 163 |
| Loja2 | 42 | 213 |
| Loja3 | 32 | 106 |
Ou, por produto:
df_vendas_preco_unit.groupby(level="Produto")[
["UnidadesVendidas", "ReceitaTotal"]
].sum()
| UnidadesVendidas | ReceitaTotal | |
|---|---|---|
| Produto | ||
| ProdutoA | 23 | 108 |
| ProdutoB | 42 | 129 |
| ProdutoC | 25 | 159 |
| ProdutoD | 24 | 86 |
Ou, ainda, por loja a cada mês:
df_vendas_preco_unit.groupby(level=["Data", "Loja"])[
["UnidadesVendidas", "ReceitaTotal"]
].sum()
| UnidadesVendidas | ReceitaTotal | ||
|---|---|---|---|
| Data | Loja | ||
| 2022-01-31 | Loja1 | 20 | 102 |
| Loja2 | 18 | 76 | |
| Loja3 | 12 | 60 | |
| 2022-02-28 | Loja1 | 20 | 61 |
| Loja2 | 24 | 137 | |
| Loja3 | 20 | 46 |
Por produto a cada mês:
df_vendas_preco_unit.groupby(level=["Data", "Produto"])[
["UnidadesVendidas", "ReceitaTotal"]
].sum()
| UnidadesVendidas | ReceitaTotal | ||
|---|---|---|---|
| Data | Produto | ||
| 2022-01-31 | ProdutoA | 8 | 49 |
| ProdutoB | 19 | 53 | |
| ProdutoC | 13 | 84 | |
| ProdutoD | 10 | 52 | |
| 2022-02-28 | ProdutoA | 15 | 59 |
| ProdutoB | 23 | 76 | |
| ProdutoC | 12 | 75 | |
| ProdutoD | 14 | 34 |
O tipo de agrupamento vai depender do interesse, assim como a operação de
agrupamento (soma, média, etc). O foco aqui é entender quando se usa axis=0 ou
axis=1 e entender que, no Pandas, a ideia de dimensões superiores é dada pelos
índices.
Conclusão #
A compreensão do conceito de eixo (axis) é essencial para o trabalho com dados em bibliotecas como NumPy e Pandas. No NumPy, o eixo é usado para indicar a dimensão ao longo da qual uma operação deve ser aplicada em um array. Já no Pandas, que é uma biblioteca voltada para dados tabulares, o eixo é usado para operações em colunas ou linhas.
Vimos que o NumPy pode lidar com arrays de diferentes dimensões, desde 1D até 4D ou mais, enquanto o Pandas é voltado para dados tabulares 2D. No entanto, o Pandas permite criar índices com múltiplos níveis, o que permite organizar os dados em mais dimensões sem a necessidade de estruturas de dados complexas.
Esperamos que este artigo tenha ajudado a esclarecer as diferenças entre os conceitos de eixo no NumPy e Pandas e como eles podem ser aplicados no trabalho com dados em Python.
Até a próxima!

