Engenheiros e cientistas sempre buscam extrair o máximo de desempenho de seus equipamentos e projetos com o mínimo de custo. Essa busca dá origem aos chamados problemas de otimização. Neste artigo, veremos como podemos utilizar a linguagem Python, com auxílio do pacote SymPy, na resolução de tais problemas.
Entendendo um problema de otimização #
Comecemos entendendo a essência de um problema de otimização do ponto de vista matemático. Podemos entender otimização como sendo a busca por uma entrada para uma função \(f(x)\) tal que o resultado seja o melhor valor de saída para a \(f(x)\). E o que seria esse “melhor valor”? Geralmente, significa o valor máximo (se a função representa algo positivo como, por exemplo, lucro), ou o valor mínimo (se a função representa algo indesejado, como custo).
No artigo sobre derivadas com Python, vimos que a derivada de uma função possui relação com a inclinação de uma reta tangente à função em um dado ponto. Assim, quando \(f’(x) = 0\), tal inclinação é nula indicando que se está em um ponto de máximo ou de mínimo. Pontos que satisfazem a igualdade anterior são chamados de pontos críticos de uma função.
Já a derivada segunda, \(f’’(x)\), tem relação com a curvatura de \(f(x)\) e podemos a utilizar para verificar se um dado ponto crítico é de máximo ou de mínimo. Se \(f’’(x) < 0\), a função é um máximo; se \(f’’(x) > 0\), a função é um mínimo; já se \(f’’(x) = 0\), a função está em um ponto de inflexão, mudando de uma região de máximo para uma de mínimo, ou vice-versa.
Vamos partir para um exemplo. Considere a seguinte função:
$$ f(x) = x^3 - 2x^2 + x $$Vamos criá-la com o SymPy:
# configuração para outputs melhores no artigo, pode ser ignorado
from sympy import init_printing
init_printing(scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
# importando o necessário para este início de artigo
from sympy import Symbol, diff, solve, plot
# criando o símbolo da variável e a função
x = Symbol('x')
f = x**3 - 2*x**2 +x
f
\(\displaystyle x^{3} - 2 x^{2} + x\)
Podemos facilmente com a função diff do SymPy obter as derivadas primeira e
segunda:
derivada_primeira = diff(f, x)
derivada_primeira
\(\displaystyle 3 x^{2} - 4 x + 1\)
derivada_segunda = diff(f, x, 2)
derivada_segunda
\(\displaystyle 2 \left(3 x - 2\right)\)
Com a função solve, podemos obter os pontos críticos resolvendo a primeira
derivada para x. Ou seja, resolvendo \(f’(x)=0\):
pontos_criticos = solve(derivada_primeira, x)
pontos_criticos
\(\displaystyle \left[ \frac{1}{3}, \ 1\right]\)
Observe que o resultado sai em forma de uma lista. Podemos substituir cada resultado obtido na expressão da derivada segunda:
derivada_segunda.subs({x: pontos_criticos[0]}), derivada_segunda.subs({x: pontos_criticos[1]})
\(\displaystyle \left( -2, \ 2\right)\)
E verificar se há algum ponto de inflexão:
ponto_inflexao = solve(derivada_segunda, x)
ponto_inflexao
\(\displaystyle \left[ \frac{2}{3}\right]\)
Vemos que \(f’’(\frac{1}{3}) < 0\), indicando ser um ponto de máximo, e que \(f’’(1) > 0\), sendo um ponto de mínimo. Em \(x = \frac{2}{3}\) há mudança de concavidade da função.
Vejamos o gráfico da função:
plot(f, (x, -0.2, 1.2));
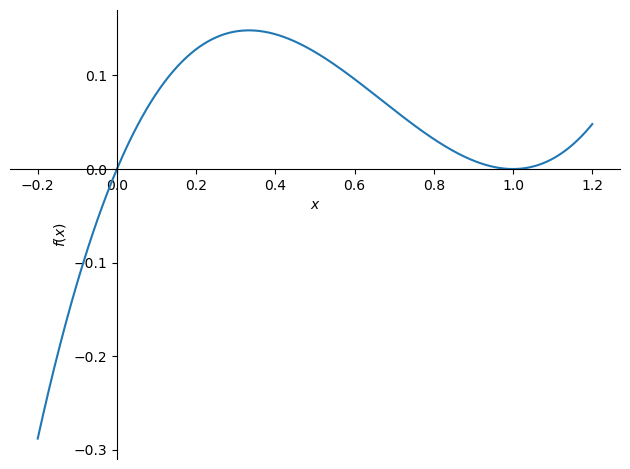
Veja que o gráfico foi propositalmente construído em um intervalo (domínio) tal que fica evidente o máximo e o mínimo. No entanto, observe que a função é crescente para \(x > 1\) e decrescente para \(x < 0\). Daí a importância de se definir um domínio de validade para o problema logo no início. Supondo um domínio tal que \(x \in [0, 1]\) podemos afirmar que \((\frac{1}{3}, f(\frac{1}{3}))\) é um ponto de máximo.
Exemplo de aplicação - minimizando custos #
Vamos pegar um exemplo bem comum em processos químicos: a minimização do custo de construção de um tanque. Aliás, sou químico de formação, já escrevi aqui um pouco de como a tecnologia influenciou minha carreira, assim como certamente influencia a sua. Para mais detalhes de meus projetos, veja meu portfolio.
Obtendo nossa função #
Em nosso exemplo, consideraremos um tanque cilíndrico de volume fixo (V) e desejamos determinar o comprimento (L) e o diâmetro (D) que minimizam o custo do tanque. O custo por unidade de área da lateral do tanque é \(c_s\) e o custo por unidade de área do topo e do fundo do tanque é \(c_t\). Com um pouco de geometria básica apresentada na figura a seguir, conseguir obter nossa função \(f\) que representa o custo:
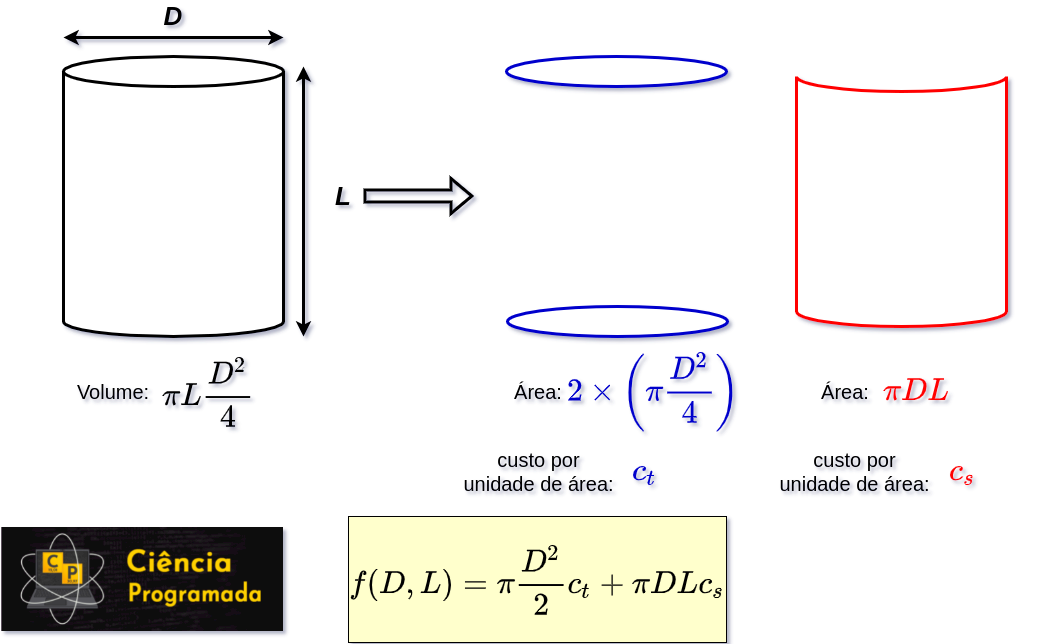
Vamos criar os símbolos necessários para representar nossa função. Observe que em todos foi colocada a restrição de que são valores positivos, já que não faz sentido falar em dimensões ou custos negativos. É importante lembrar de avaliar restrições em problemas de otimização.
from sympy import pi
diametro = Symbol('D', positive=True)
comprimento = Symbol('L', positive=True)
volume = Symbol('V', positive=True)
custo_lado = Symbol('c_s', positive=True)
custo_topo = Symbol('c_t', positive=True)
f = custo_lado * pi * diametro * comprimento + custo_topo * (pi / 2) * diametro**2
f
\(\displaystyle \frac{\pi D^{2} c_{t}}{2} + \pi D L c_{s}\)
Vamos considerar que não há limite para os valores e buscar uma expressão em função de V e de D. Assim, eliminando L da expressão:
volume_cilindro = (pi / 4) * diametro**2 * comprimento
volume_cilindro
\(\displaystyle \frac{\pi D^{2} L}{4}\)
comprimento_funcao_volume = solve(volume_cilindro - volume, comprimento)[0]
comprimento_funcao_volume
\(\displaystyle \frac{4 V}{\pi D^{2}}\)
f = f.subs({comprimento: comprimento_funcao_volume})
f
\(\displaystyle \frac{\pi D^{2} c_{t}}{2} + \frac{4 V c_{s}}{D}\)
Logo, a expressão acima é a que queremos otimizar, obtendo um valor mínimo. Vamos obter a expressão de sua derivada primeira em relação ao diâmetro:
f_min = diff(f, diametro)
f_min
\(\displaystyle \pi D c_{t} - \frac{4 V c_{s}}{D^{2}}\)
Agora, podemos obter uma expressão para o diâmetro que torna a derivada nula:
diametro_otimo = solve(f_min, diametro)[0]
diametro_otimo
\(\displaystyle \frac{2^{\frac{2}{3}} \sqrt[3]{V} \sqrt[3]{c_{s}}}{\sqrt[3]{\pi} \sqrt[3]{c_{t}}}\)
E, com o diâmetro, obter o comprimento otimizado:
comprimento_otimo = comprimento_funcao_volume.subs({diametro: diametro_otimo}).simplify()
comprimento_otimo
\(\displaystyle \frac{2^{\frac{2}{3}} \sqrt[3]{V} c_{t}^{\frac{2}{3}}}{\sqrt[3]{\pi} c_{s}^{\frac{2}{3}}}\)
Vejamos qual a razão comprimento / diâmetro que minimiza o custo:
comprimento_otimo / diametro_otimo
\(\displaystyle \frac{c_{t}}{c_{s}}\)
Veja que resultado interessante. Se os custos forem os mesmos, o cilindro que minimiza o custo é aquele que possui comprimento igual ao diâmetro da base, já que a razão acima teria valor 1. Escreveremos mais sobre isso adiante.
Vamos colocar valores de exemplo para visualizar melhor nosso resultado. Vamos considerar os custos iguais a 1 unidade e o volume igual a 10 unidades. O diâmetro que minimiza a função é:
solve(f_min.subs({custo_lado: 1, custo_topo: 1, volume: 10}), diametro)[0]
\(\displaystyle \frac{2 \sqrt[3]{5}}{\sqrt[3]{\pi}}\)
Que, numericamente, corresponde a:
# o _ permite recuperar o valor da célula anterior
_.n()
\(\displaystyle 2.33508864988147\)
Vejamos o gráfico de nossa função custo:
p = plot(f.subs({custo_lado: 1, custo_topo: 1, volume: 10}),
(diametro, 0, 5), ylim=(0, 100), legend=True, show=False)
p[0].label = 'f'
p.show()
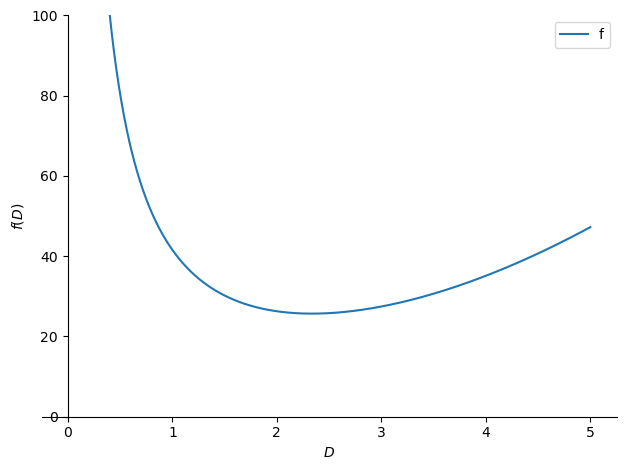
Veja como realmente há um mínimo ao redor do diâmetro 2,33. Logo, este é o diâmetro (e também o comprimento) para as condições de contorno fornecidas.
E se os custos forem distintos? #
O que acontece se os custos forem distintos? Vamos considerar o custo da lateral do tanque como o dobro do custo de topo:
solve(f_min.subs({custo_lado: 2, custo_topo: 1, volume: 10}), diametro)[0]
\(\displaystyle \frac{2 \sqrt[3]{10}}{\sqrt[3]{\pi}}\)
_.n()
\(\displaystyle 2.94202734335627\)
Veja que o diâmetro da base aumentou comparado ao caso anterior. Consequentemente, como a razão comprimento / diâmetro depende apenas dos custos, o comprimento é metade do diâmetro obtido. Consegue agora entender o formato “achatado” dos cilindros que armazenam líquidos que costumamos ver em plantas industriais?
Nesses cilindros a pressão interna do líquido é dada pela famosa equação \(P = \rho g h\), ou seja, depende da densidade do líquido, da gravidade e da altura da coluna de líquido. Logo, um tanque alto levaria à necessidade de se ter paredes mais grossas para aguentar a pressão do líquido. E, claro, isso afeta muito os custos de construção, especialmente das paredes laterais. Simples, não? Claro que há muito mais envolvido, como pode ser visto aqui.
E todos esses formatos diferentes para latas de alimentos? #
Vimos nas contas acima que, se os custos da lateral e do topo forem iguais, o formato cilíndrico que minimiza o custo total é aquele com diâmetro da base igual ao comprimento do cilindro. Mas, então, por que tal formato é tão raro em enlatados que vemos no mercado? Aliás, primeiramente, por que cilindro?
Em nossas contas, consideramos implicitamente que o custo decorre apenas da área. Logo, por que então não usar recipientes esféricos? Afinal, uma das primeiras coisas ensinadas em aulas de geometria é que a esfera tem a menor área superficial dentre todas as formas fechadas ao redor de um volume. OK, legal… Agora tente empilhar diversos recipientes esféricos em uma prateleira de mercado. Boa sorte :-)
Além do fato de que esferas rolam muito facilmente, seu empacotamento é pouco efetivo. No máximo conseguimos ocupar 74 % do espaço disponível empilhando esferas. Procure seu químico de confiança mais próximo se quiser uma demonstração matemática disso. Assim, fica claro que outras considerações estão envolvidas no assunto. Não é apenas o custo de construção, há também o de transporte, armazenamento e disposição. Nesse sentido, formatos mais cilíndricos acabam sendo mais interessantes. Além do fator ergonômico, seu cliente precisa ser capaz de segurar o que vai consumir. Já pensou ter que segurar uma latinha de refrigerante com as duas mãos por ter um diâmetro grande?
No processo de manufatura de latas, o maior desperdício é no topo e no fundo pela necessidade de cortes e solda. Claro que há reciclagem, mas isso faz com que o custo seja distinto, sendo que nesse caso o custo da lateral é menor fazendo sentido latas mais altas.
Conclusão #
Além de cálculo e programação, também tivemos um curso rápido sobre embalagens ;-)
Vimos os cuidados que devem ser tomados em problemas de otimização, desde a correta identificação do domínio, passando pelas condições de contorno e análise crítica dos resultados obtidos. E todo o processo foi bem ágil pelo uso do SymPy.
Até a próxima.

