As equações de balanço de massa são importantes para praticamente todos os cálculos na resolução de problemas de engenharia química. Sendo assim, estarão presentes durante todo o curso de graduação e carreira profissional. Balanços de massa são conduzidos durante operações de plantas de processamento ao longo de diferentes períodos de tempo, com o objetivo de controlar os processos, manter a produção e aumentar a eficiência.
Nesse artigo, vamos resolver duas questões de balanço de massa utilizando a biblioteca SymPy e revisar alguns princípios importantes.
O Conceito de Balanço de Massa #
O balanço de massa é a aplicação da Lei de Conservação de Massa:
Portanto, quando o processo for contínuo e operar em regime estacionário, o acúmulo no interior de um equipamento é zero:
Lembrando, um processo contínuo é quando há, continuamente, a passagem de massa através das fronteiras do sistema. Enquanto que um processo estacionário é quando não há alteração nos valores das variáveis de processo com o tempo.
Com uma equação relativamente simples é possível representar, de forma geral, o balanço de qualquer grandeza:
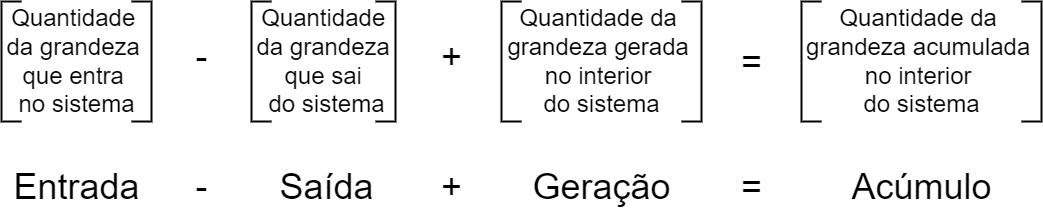
Em termos de balanço de uma grandeza em relação às fronteiras do sistema:
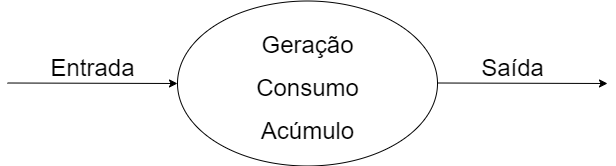
Analisando um caso real #
Vamos analisar um problema simples. Suponha que 100 mol/h de uma mistura com 30% do componente A e 70% do componente B é separada por destilação em duas frações. A corrente de topo contém 70% do componente A e na corrente de fundo há 20% do componente B. Vamos calcular a vazão molar de cada corrente.
O primeiro passo para solucionar um problema de balanço molar é ilustrar o diagrama do processo especificando as fronteiras e adicionando as variáveis conhecidas:
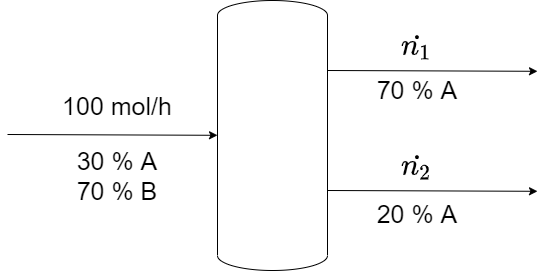
Após analisar a figura, observamos que há cruzamento através das fronteiras do processo, logo, esse problema opera em um processo contínuo. E, os valores das variáveis de processo não alteram com o tempo, consequentemente, está em regime estacionário. Além disso, notamos que não ocorre reação química.
Resolvendo com Python e SymPy #
Para resolver o problema, vamos importar as bibliotecas que usaremos:
from collections import namedtuple
import sympy
sympy.init_printing(use_latex='png', scale=1.05, order='grlex',
forecolor='Black', backcolor='White', fontsize=10)
Vamos começar criando as variáveis com as informações do enunciado e completar com as frações molares que não foram fornecidas, mas que são facilmente determinadas através das seguintes restrições:
$$ \begin{aligned} x_a+x_b=1 \Rightarrow 0,7+x_b=1 \Rightarrow x_b=0,3 \\ y_a+y_b=1 \Rightarrow 0,2+y_b=1 \Rightarrow y_b=0,8 \end{aligned} $$Onde xa é a fração molar do componente A e xb a fração molar do componente B, ambos na corrente de topo. ya é a fração molar do componente A e yb a fração molar do componente B, ambos na corrente de fundo.
feed_rate = 100 # vazão molar em mol/h
Composition = namedtuple('Composition', 'A B')
feed = Composition(0.3, 0.7) # composição da alimentação
stream_1 = Composition(0.7, 0.3) # composição da corrente de topo
stream_2 = Composition(0.2, 0.8) # composição da corrente de fundo
Observe que utilizei a função namedtuple. Essa função permite acessar os
valores usando os nomes dos campos ao invés dos índices de posição de uma
tupla, o que deixa o código mais legível. Caso não tenha ficado claro, veremos
a aplicação disso logo a seguir.
Agora, vamos identificar os símbolos de vazão molar utilizando LaTeX. Geralmente utilizamos um ponto acima do símbolo de vazão para identificar uma taxa. Logo, a vazão molar (\(\dot{n}\)) de uma corrente de processo é o número de mols (\(n\)) transportado por unidade de tempo.
$$ \dot{n} = \frac{n}{t} $$flow_rate_1, flow_rate_2 = sympy.symbols('\dot{n_1} \dot{n_2}')
flow_rate_1, flow_rate_2
\( (\dot{n_1}, \ \dot{n_2}) \)
O próximo passo é escrever as equações que precisamos resolver em termos das variáveis conhecidas e das incógnitas. Como nesse problema não há presença de reação química e envolve balanço molar em regime estacionário, temos:
Que é coerente com o que escrevemos no início do artigo sobre o termo de acúmulo no interior de um equipamento ser zero:
Portanto, no caso do nosso exercício, o balanço molar global é:
$$\dot{n_1}+\dot{n_2}=100$$E o balanço molar por componentes é:
$$ \begin{aligned} 0,7\cdot\dot{n_1}+0,2\cdot\dot{n_2}=0,3\cdot100 \quad \text{ (componente A)} \\ 0,3\cdot\dot{n_1}+0,8\cdot\dot{n_2}=0,7\cdot100 \quad \text{ (componente B)} \end{aligned} $$Precisamos passar essas informações para o SymPy, criando um sistema de equações. Já escrevemos sobre isso neste artigo, vamos aplicar ao nosso exercício:
system = (sympy.Eq(flow_rate_1 + flow_rate_2, feed_rate), # global
sympy.Eq(stream_1.A * flow_rate_1 + stream_2.A * flow_rate_2, feed.A * feed_rate), # componente A
sympy.Eq(stream_1.B * flow_rate_1 + stream_2.B * flow_rate_2, feed.B * feed_rate) # componente B
)
# mostrando cada equação do sistema
for equation in system:
display(equation)
Em Python os símbolos = e == são operadores de atribuição e igualdade,
respectivamente, e não podemos utilizá-los para criar a igualdade em equações.
Para configurar uma equação o SymPy tem a função Eq, que cria uma igualdade
simbólica.
Outro fato importante é que conseguimos perceber a vantagem de usar a função
namedtuple quando chamamos os componentes. Nomeamos os campos como A e B e
acessamos os valores utilizando a notação de ponto, o que melhora a legibilidade
do código.
Com o sistema criado, basta solicitar que o mesmo seja resolvido com a função
solve do SymPy:
solution = sympy.solve(system)
solution
\( { \dot{n_1}: 20.0, \ \dot{n_2}: 80.0 } \)
Então, temos a corrente de topo com vazão de 20 mol/h e a corrente de fundo com vazão de 80 mol/h.
Essa linha de raciocínio se aplica a qualquer quantidade de componentes. Desde que o número de variáveis seja igual ou maior que o de equações, o sistema pode ser resolvido. Vejamos mais um exemplo, desta vez com 3 correntes de saída e 3 componentes.
Um caso real com mais componentes #
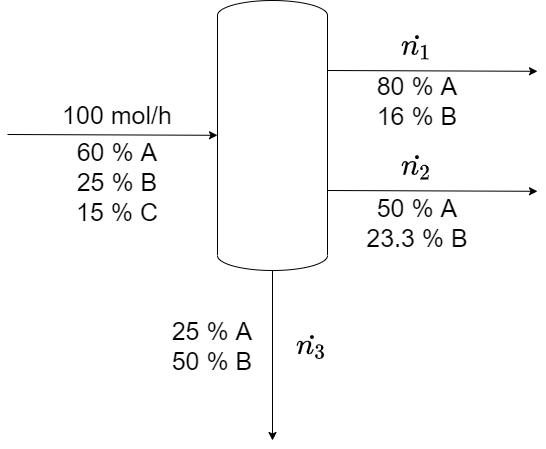
Suponha que 100 mol/h de uma mistura com 60% do componente A, 25% do componente B e 15% do componente C é separada por destilação em três frações. As correntes contêm:
i) 80% do componente A e 16% do componente B;
ii) 50% do componente A e 23,3% do componente B;
iii) 25% do componente A e 50% do componente B.
Vamos calcular a vazão molar de cada corrente. Para isso, começamos ilustrando o diagrama do processo especificando as fronteiras e adicionando as variáveis conhecidas:
Resolvendo com Python e SymPy #
Precisamos criar as variáveis com as informações necessárias para resolver o problema. Vamos extrair esses dados do enunciado e as frações molares restantes conseguimos determinar através das seguintes restrições:
$$ \begin{aligned} x_a+x_b+x_c=1 & \Rightarrow 0,8+0,16+x_c=1 && \Rightarrow x_c=0,04 \\ y_a+y_b+y_c=1 & \Rightarrow 0,5+0,233+y_c=1 && \Rightarrow y_c=0,267 \\ z_a+z_b+z_c=1 & \Rightarrow 0,25+0,5+z_c=1 && \Rightarrow y_c=0,25 \end{aligned} $$feed_rate = 100 # vazão molar em mol/h
Composition = namedtuple('Composition', 'A B C')
feed = Composition(0.6, 0.25, 0.15) # composição da alimentação
stream_1 = Composition(0.8, 0.16, 0.04) # composição da corrente de topo
stream_2 = Composition(0.5, 0.233, 0.267) # composição da corrente do meio
stream_3 = Composition(0.25, 0.5, 0.25) # composição da corrente de fundo
Agora, vamos identificar os símbolos de vazão molar utilizando LaTeX:
flow_rate_1, flow_rate_2, flow_rate_3 = sympy.symbols('\dot{n_1} \dot{n_2} \dot{n_3}')
flow_rate_1, flow_rate_2, flow_rate_3
\( \dot{n_1}, \ \dot{n_2}, \ \dot{n_3} \)
Nesse problema:
Baseado nisso, vamos escrever as equações que precisamos resolver. A linha de raciocínio é a mesma do caso anterior, só aumenta o número de variáveis e equações.
O balanço molar global é:
$$\dot{n_1}+\dot{n_2}+\dot{n_3}=100$$E o balanço molar por componentes é:
$$ \begin{aligned} 0,8\cdot\dot{n_1}+0,5\cdot\dot{n_2}+0,25\cdot\dot{n_3}=0,6\cdot100 \quad \text{ (componente A)} \\ 0,16\cdot\dot{n_1}+0,233\cdot\dot{n_2}+0,5\cdot\dot{n_3}=0,25\cdot100 \quad \text{ (componente B)} \\ 0,04\cdot\dot{n_1}+0,267\cdot\dot{n_2}+0,25\cdot\dot{n_3}=0,15\cdot100 \quad \text{ (componente C)} \end{aligned} $$Agora vamos passar essas informações para o SymPy, criando um sistema de equações:
system = (sympy.Eq(flow_rate_1 + flow_rate_2 + flow_rate_3, feed_rate),
sympy.Eq(stream_1.A * flow_rate_1 + stream_2.A * flow_rate_2 + stream_3.A * flow_rate_3, feed.A * feed_rate),
sympy.Eq(stream_1.B * flow_rate_1 + stream_2.B * flow_rate_2 + stream_3.B * flow_rate_3, feed.B * feed_rate),
sympy.Eq(stream_1.C * flow_rate_1 + stream_2.C * flow_rate_2 + stream_3.C * flow_rate_3, feed.C * feed_rate))
# mostrando cada equação do sistema
for equation in system:
display(equation)
Após criar o sistema precisamos solicitar que o mesmo seja resolvido com a
função solve do SymPy:
solution = sympy.solve(system)
solution
\( { \dot{n_1}: 50.0404203718674, \ \dot{n_2}: 29.9110751818917, \ \dot{n_3}: 20.0485044462409 } \)
Temos na corrente de topo a vazão de 50 mol/h, na corrente do meio a vazão de 30 mol/h, e na corrente de fundo a vazão de 20 mol/h.
Conclusão #
Ficou mais simples resolver equações de Balanço de Massa com Python, não é?! Nesse artigo, vimos como algumas funcionalidades da biblioteca SymPy automatizam a resolução de problemas de Balanço de Massa. Além disso, podemos aplicar facilmente as ferramentas utilizadas para solucionar outros tipos de balanços e problemas de engenharia química.
Este artigo é uma colaboração minha, Helena Benevenuto, com o Ciência Programada. Me acompanhe no LinkedIn para mais conteúdos de química.
Compartilhe este artigo em suas redes e siga o projeto Ciência Programada para sempre estar atualizado. Até a próxima.

