Top 3 bibliotecas Python para química
#

Estudantes e profissionais da área química precisam realizar diversos cálculos no dia a dia. Tais cálculos muitas vezes são complexos devido à grande quantidade de dados e de aproximações. Ferramentas computacionais facilitam a resolução dessas atividades.

Nesse artigo, vamos explorar 3 bibliotecas químicas disponíveis para a linguagem Python, mostrando como elas são úteis na nossa rotina.

Molmass
#

Começamos nosso Top 3 com o Molmass, um pacote Python que permite calcular a massa molar de uma forma bem simples. Ao invés de calcular tediosamente as massas molares de compostos somando as dos seus elementos constituintes, basta passar sua fórmula, como veremos.

A instalação pode ser feita via pip install molmass. E, para importar:

from molmass import Formula

Vamos começar com um exemplo simples: cerveja! Mais especificamente, o etanol presente nas cervejas.

Podemos calcular a massa molar do etanol facilmente com o Molmass. Para isso, passamos uma string com a fórmula do etanol para a classe Formula e solicitamos o atributo mass, a unidade utilizada é g/mol, como informado no comentário:

formula = Formula('C2H5OH')
formula.mass  # g/mol

46.068531

Podemos observar que o pacote utiliza as massas molares sem arredondamentos, o que é excelente, pois o uso de aproximações leva à propagação de erros.

Ah, e se quiser continuar o papo de cerveja, veja como ela já deu origem à uma biblioteca Python nesse artigo. Mas só depois de terminar este artigo aqui :-)

O Molmass aceita diferentes entradas para um mesmo composto. Vamos passar outra string com a abreviação clássica do radical etil na orgânica, Et, para obter a massa molar do etanol:

formula = Formula('EtOH')
formula.mass

46.068531

Observe que as fórmulas diferenciam maiúsculas de minúsculas.

Para obter informações da composição elementar do composto, podemos utilizar o método composition:

formula.composition()

(('C', 2, 24.02148, 0.5214292593788155),
 ('H', 6, 6.047646, 0.13127499116479316),
 ('O', 1, 15.999405, 0.34729574945639136))

Vemos que o método composition fornece colunas com os atributos element, number, relative_mass e fraction, respectivamente.

Mendeleev
#

Outro pacote Python muito útil no nosso dia a dia é o Mendeleev. Ele permite acessar várias propriedades de elementos, íons e isótopos.

O pacote pode ser instalado via pip install mendeleev.

Tabela periódica
#

Uma das caracteristicas mais legais do Mendeleev é a possibilidade de importar uma tabela periódica com apenas uma linha de código. Para isso precisamos ter a dependência vis, que pode ser instalada via pip install mendeleev[vis].

Uma maneira de visualizar a tabela periódica é usando a função periodic_table do módulo mendeleev.vis:

from mendeleev.vis import periodic_table

Para observar a visualização padrão da tabela periódica vamos chamar a função importada:

periodic_table()

Propriedades de elementos
#

Agora de um ponto de vista mais técnico. Para acessar os dados de um elemento basta importar por meio de seus símbolos. Por exemplo, considere o cromo:

from mendeleev import Cr

Para extrair alguma informação podemos solicitar um atributo, por exemplo, o boiling_point onde vamos obter a temperatura de ebulição em Kelvin, como informado no comentário:

Cr.boiling_point  # K

2945.0

Uma forma alternativa para acessar os dados é por meio do element, método que retorna uma única instância ou uma tupla dessas instâncias, dependendo dos argumentos:

from mendeleev import element

O método element aceita o nome do elemento em inglês, o símbolo atômico ou o número atômico. Vejamos um exemplo em que passamos o número atômico do bromo para o método element e solicitamos o atributo atomic_radius onde vamos obter o raio atômico em picometros, como informado no comentário:

bromo = element(35)
bromo.atomic_radius  # pm

115.0

O método element também aceita lista ou tupla. Observe esse exemplo em que passamos uma lista para o método element e solicitamos o atributo econf onde vamos obter a configuração eletronica dos elementos:

hidrogenio, zinco, bromo = element(['Hydrogen', 'Zn', 35]) 
hidrogenio.econf, zinco.econf, bromo.econf

('1s', '[Ar] 3d10 4s2', '[Ar] 3d10 4s2 4p5')

Com o Mendeleev também conseguimos obter a configuração eletrônica do íon a partir do elemento. Tomemos como exemplo o íon Fe³⁺. Primeiramente, passamos o nome do elemento em inglês para o método element e solicitamos o atributo ec onde vamos obter a configuração eletrônica do átomo de ferro:

ferro = element('Iron')
ferro.ec

<ElectronicConfiguration(conf="1s2 2s2 2p6 3s2 3p6 3d6 4s2")>

Para obter a configuração eletrônica do íon Fe³⁺ vamos utilizar o método ionize a fim de remover os 2 elétrons da última camada eletrônica ~~e não do subnível mais energético~~ e 1 elétron, ~~agora sim,~~ do subnível mais energético, retornando a seguinte configuração eletrônica:

ferro.ec.ionize(3)

<ElectronicConfiguration(conf="1s2 2s2 2p6 3s2 3p6 3d5")>

Existem alguns atributos como o isotopes que retorna uma lista de objetos com as propriedades de cada isótopo atomic_number, mass_number, mass e abundance, respectivamente:

enxofre = element('S')
for iso in enxofre.isotopes:
    print(iso)

   16    32   31.97207 0.944
   16    33   32.97146 0.008
   16    34   33.96787 0.048
   16    36   35.96708 0.000

O ionic_radii retorna uma lista de objetos com os atributos charge, coordination, crystal_radius em pm, e ionic_radius em pm:

ouro = element('Au')
for ir in ouro.ionic_radii:
    print(ir)

charge=   1, coordination=VI   , crystal_radius=151.000, ionic_radius=137.000
charge=   3, coordination=IVSQ , crystal_radius=82.000, ionic_radius=68.000
charge=   3, coordination=VI   , crystal_radius=99.000, ionic_radius=85.000
charge=   5, coordination=VI   , crystal_radius=71.000, ionic_radius=57.000

O ionenergies retorna um dicionário com energias de ionização:

oxigenio = element('O')
oxigenio.ionenergies

{1: 13.618054,
 2: 35.12111,
 3: 54.93554,
 4: 77.4135,
 5: 113.8989,
 6: 138.1189,
 7: 739.32679,
 8: 871.40985}

Outro atributo é o oxistates que retorna uma lista dos estados de oxidação mais comuns para um determinado elemento:

manganes = element('Mn')
manganes.oxistates

[7, 6, 4, 3, 2]

O método element possui vários outros atributos e/ou métodos que nos permitem acessar diversas propriedades dos elementos. Vamos observar todos os disponíveis no objeto manganes que criamos:

manganes = element('Mn')
[x for x in dir(manganes) if not x.startswith('_')]

['abundance_crust',
 'abundance_sea',
 'annotation',
 'atomic_number',
 'atomic_radius',
 'atomic_radius_rahm',
 'atomic_volume',
 'atomic_weight',
 'atomic_weight_uncertainty',
 'block',
 'boiling_point',
 'c6',
 'c6_gb',
 'cas',
 'covalent_radius',
 'covalent_radius_bragg',
 'covalent_radius_cordero',
 'covalent_radius_pyykko',
 'covalent_radius_pyykko_double',
 'covalent_radius_pyykko_triple',
 'cpk_color',
 'density',
 'description',
 'dipole_polarizability',
 'dipole_polarizability_unc',
 'discoverers',
 'discovery_location',
 'discovery_year',
 'ec',
 'econf',
 'electron_affinity',
 'electronegativity',
 'electronegativity_allen',
 'electronegativity_allred_rochow',
 'electronegativity_cottrell_sutton',
 'electronegativity_ghosh',
 'electronegativity_gordy',
 'electronegativity_li_xue',
 'electronegativity_martynov_batsanov',
 'electronegativity_mulliken',
 'electronegativity_nagle',
 'electronegativity_pauling',
 'electronegativity_sanderson',
 'electronegativity_scales',
 'electrons',
 'electrophilicity',
 'en_allen',
 'en_ghosh',
 'en_pauling',
 'evaporation_heat',
 'fusion_heat',
 'gas_basicity',
 'geochemical_class',
 'glawe_number',
 'goldschmidt_class',
 'group',
 'group_id',
 'hardness',
 'heat_of_formation',
 'init_on_load',
 'ionenergies',
 'ionic_radii',
 'is_monoisotopic',
 'is_radioactive',
 'isotopes',
 'jmol_color',
 'lattice_constant',
 'lattice_structure',
 'mass',
 'mass_number',
 'mass_str',
 'melting_point',
 'mendeleev_number',
 'metadata',
 'metallic_radius',
 'metallic_radius_c12',
 'molcas_gv_color',
 'name',
 'name_origin',
 'neutrons',
 'nvalence',
 'oxides',
 'oxistates',
 'period',
 'pettifor_number',
 'proton_affinity',
 'protons',
 'registry',
 'sconst',
 'screening_constants',
 'series',
 'softness',
 'sources',
 'specific_heat',
 'symbol',
 'thermal_conductivity',
 'uses',
 'vdw_radius',
 'vdw_radius_alvarez',
 'vdw_radius_batsanov',
 'vdw_radius_bondi',
 'vdw_radius_dreiding',
 'vdw_radius_mm3',
 'vdw_radius_rt',
 'vdw_radius_truhlar',
 'vdw_radius_uff',
 'zeff']

Propriedades de íons
#

O mendeleev possui a classe Ion para trabalhar com íons ao invés de elementos. Os íons podem ser criados a partir de elementos e informações de carga:

from mendeleev.ion import Ion

ferro_3 = Ion("Fe", 3)

Vamos acessar algumas propriedades dos íons:

ferro_3.electrons

ferro_3.name

'Iron 3+ ion'

ferro_3.unicode_ion_symbol()

'Fe³⁺'

ChemPy
#

ChemPy é um pacote Python que permite resolver problemas de química analítica, físico-química e inorgânica.

O pacote pode ser instalado via pip install chempy.

Balanceamento de equações
#

Com o ChemPy podemos balancear os coeficientes estequiométricos de uma reação. Para importar, simplesmente:

from chempy import balance_stoichiometry

Vamos imaginar um exemplo em que precisamos balancear a reação de combustão do acetileno, gás combustível empregado em maçaricos.

$$ C_2H_2 + O_2 \rightarrow CO_2 + H_2O $$

Para isso, passamos os reagentes e os produtos para a função balance_stoichiometry:

balance_stoichiometry({'C2H2', 'O2'}, {'CO', 'H2O'})

(OrderedDict([('C2H2', 2), ('O2', 3)]), OrderedDict([('CO', 4), ('H2O', 2)]))

Obtivemos dois dicionários, um para os reagentes e outro para os produtos, com os coeficientes estequiométricos que balanceiam a equação.

Vamos agora considerar outro exemplo para mostrar que podemos obter a equação balanceada diretamente. Balancearemos a seguinte reação, que é utilizada em boosters de foguetes espaciais para auxiliar no lançamento dos mesmos:

$$ NH_4ClO_4 + Al \rightarrow Al_2O_3 + HCl + H_2O + N_2 $$

reac, prod = balance_stoichiometry({'NH4ClO4', 'Al'}, {'Al2O3', 'HCl', 'H2O', 'N2'})

reac

OrderedDict([('Al', 10), ('NH4ClO4', 6)])

prod

OrderedDict([('Al2O3', 5), ('H2O', 9), ('HCl', 6), ('N2', 3)])

Dessa maneira retorna um dicionário ordenado, solicitando a função dict criamos um dicionário padrão:

dict(reac)

{'Al': 10, 'NH4ClO4': 6}

dict(prod)

{'Al2O3': 5, 'H2O': 9, 'HCl': 6, 'N2': 3}

Podemos construir a equação balanceada usando a classe Reaction:

from chempy import Reaction

reaction = Reaction(reac, prod)
reaction

10 Al + 6 NH4ClO4 -> 5 Al2O3 + 9 H2O + 6 HCl + 3 N2

Sistemas redox
#

Dentre os experimentos mais bonitos e interessantes de química temos as reações que mudam de cor. Esses experimentos de mudança de cor podem ocorrer, por exemplo, como resultado de reações de redução e oxidação.

KMnO4 — Reação de permanganato de potássio com peróxido de hidrogênio

No exemplo do GIF, a mudança de cor ocorre devido íons roxos de permanganato, MnO₄^-, receberem elétrons para formar íons incolores de manganês(II), Mn⁺². Além disso, a formação de gás ocorre porque o peróxido de hidrogênio, H₂O₂, e o oxigênio do MnO₄^- são convertidos em H₂O e O₂.

Caso você precise balancear essa reação redox, também conseguimos com o ChemPy. Vamos obter a equação global balanceada das seguintes semi-reações:

$$ \begin{align*} MnO_4^- + 8H^+ + 5e^- &\rightleftharpoons Mn^{+2} + 4H_2O \\ H_2O_2 &\rightleftharpoons O_2 + 2H^+ + 2e^- \end{align*} $$

Para isso passamos os reagentes e os produtos das respectivas semi-reações para a classe Equilibrium:

from chempy import Equilibrium

sr_red = Equilibrium({'MnO4-': 1, 'H+': 8, 'e-': 5}, {'Mn+2': 1, 'H2O': 4})
sr_ox = Equilibrium({'H2O2': 1}, {'O2': 1, 'H+':2, 'e-':2})

Agora precisamos eliminar os elétrons e multiplicar cada reação pelos seus respectivos coeficientes para obter a equação global balanceada:

coeff = Equilibrium.eliminate([sr_red, sr_ox], 'e-')
coeff

[2, 5]

redox = sr_red * coeff[0] + sr_ox * coeff[1]
redox

6 H+ + 5 H2O2 + 2 MnO4- -> 8 H2O + 2 Mn+2 + 5 O2

Cinética química
#

Além de balanceamento, o Chempy é muito útil no estudo de cinética química.

A equação de Arrhenius fornece a dependência da constante de velocidade com a temperatura como:

$$ k = A \exp \left( -\frac{E_a}{RT} \right) $$

Tomando o logaritmo natural da equação de Arrhenius e reorganizando a equação, temos a forma de uma equação linear:

$$ \ln k = - \frac{E_a}{R}\frac{1}{T} + \ln A $$

O ChemPy possibilita obter a energia de ativação e o parâmetro A utilizando a função fit_arrhenius_equation. Vamos começar importando a função:

from chempy.kinetics.arrhenius import fit_arrhenius_equation

Agora vamos passar um conjunto de valores de temperatura em Kelvin, de constante de velocidade em L/(mol.s) e erros da constante de velocidade. Para isso, vamos importar a biblioteca NumPy a fim de criar os arrays e para usar posteriormente as funções logaritmo natural (log) e exponencial (exp):

import numpy as np

temperatures = np.array((1125, 1053, 1001, 838))    # K
k_values = np.array((11.59, 1.67, 0.380, 0.0011))   # L / (mol.s)
k_errors = np.array((1E-2, 1E-2, 1E-3, 1E-5))

Passando as variáveis temperatures, k_values e k_errors para a função fit_arrhenius_equation vamos obter os valores da energia de ativação e do parâmetro A:

fit = fit_arrhenius_equation(temperatures, k_values, kerr=k_errors)
fit

(array([5.13001705e+12, 2.51435472e+05]),
 array([[inf, inf],
        [inf, inf]]))

Internamente, fit_arrhenius_equation utiliza o método curve_fit do SciPy. O retorno são dois arrays. O primeiro com os valores dos parâmetros; o segundo com as covariâncias quando forem possíveis de serem calculadas.

Para criar as variáveis do parâmetro A e da energia de ativação vamos acessar os elementos do primeiro array, para isso é bem simples. O primeiro array é ([5.13001705e+12, 2.51435472e+05]) cujos valores podem ser acessados como segue:

A = fit[0][0]

activation_energy = fit[0][1]

print(f'A = {A:.3e} L/(mol.s) \nEa = {activation_energy:.3e} J/mol')

A = 5.130e+12 L/(mol.s) 
Ea = 2.514e+05 J/mol

Também podemos obter a energia de ativação e o parâmetro A com a representação gráfica de $\ln k$ vs $\frac{1}{T}$.

import matplotlib.pyplot as plt
from scipy.stats import linregress

# plot config
params = {
    'lines.linewidth': 2.0,
    'axes.facecolor': 'white',
    'figure.facecolor': 'white',
    'axes.labelsize': 14,
    'axes.titlesize': 16,    
    'xtick.labelsize': 12,
    'ytick.labelsize': 12,
    'figure.autolayout': True,
    'figure.titlesize': 18,    
    'figure.figsize': (12, 6),
    'legend.shadow': False,    
    'legend.fontsize': 14,
}

plt.rcParams.update(params)

# data points
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2)
ax1.errorbar(temperatures, k_values, yerr=k_errors, marker='o', linestyle='')
ax2.scatter(1/temperatures, np.log(k_values), label='Data')

# regression
slope, intercept, r_value, p_value, std_err = linregress(1/temperatures, np.log(k_values))
regression = slope * 1/temperatures + intercept
ax2.plot(1/temperatures, regression, 
         color='red', alpha=0.5,
         label=r'$\ln k={:.0f}\frac{{1}}{{T}}+{:.2f}$'.format(slope,intercept))
ax2.legend()

# visuals
for ax in (ax1, ax2):
    ax.ticklabel_format(style='sci', axis='x', scilimits=(0,0))
    ax.xaxis.major.formatter._useMathText = True
    ax.figure.canvas.draw()
    order_magnitude = ax.xaxis.get_offset_text().get_text().replace('\\times', '')    
    ax.xaxis.offsetText.set_visible(False)
    if ax == ax1:
        ax.set_xlabel(r'$T$ / ' + order_magnitude + ' $K$', )
        ax.set_ylabel(r'$k / \frac{\ell}{mol \cdot s}$')
        ax.set_title('Forma exponencial', color='dimgray')
    else:
        ax.set_xlabel(r'$\frac{1}{T}$ / ' + order_magnitude + ' $K^{-1}$', )
        ax.set_ylabel(r'$\ln k$')
        ax.set_title('Forma linearizada', color='dimgray')

plt.suptitle('Gráficos para a equação de Arrhenius', 
             color='dimgray')
plt.show()

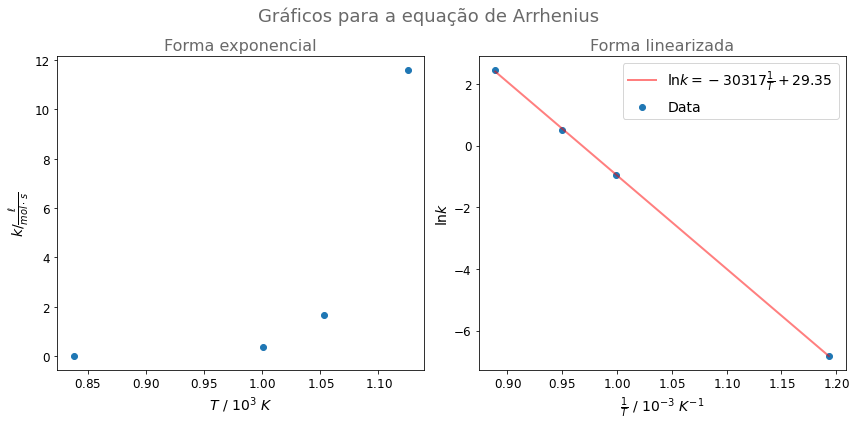
Caso queira ver como o gráfico foi gerado com a biblioteca Matplotlib veja esse repositório.

Sistemas em equilíbrio
#

O ChemPy também permite efetuar cálculos de pH. Imagine um exemplo em que precisamos descobrir o pH de uma solução 0,015 mol/L de acetato.

$$ \begin{align*} H_3CCOOH &\rightleftharpoons H^+ + H_3CCOO^- && K_a = 10^{-4.756} \\ H_2O &\rightleftharpoons H^+ + OH^- && K_w = 10^{-14} \\ \end{align*} $$

Vamos começar criando um sistema com as equações de equilíbrio e suas constantes:

from chempy.equilibria import EqSystem

equation = 'H3CCOOH = H+ + H3CCOO-; 10**-4.756'
water_autoionization = 'H2O = H+ + OH-; 10**-14/55.5'

system = EqSystem.from_string('\n'.join((equation, water_autoionization)))

Para o ChemPy conseguir resolver o sistema e fornecer as concentrações de todas as espécies em solução, precisamos passar as concentrações das espécies que são conhecidas. A concentração de acetato é de 0,015 mol/L e a concentração molecular da água é de 55,5 mol/L:

from collections import defaultdict

condition = defaultdict(float, {'H2O': 55.5, 'H3CCOO-': 0.015})

concentrations, _, _ = system.root(condition)
result = dict(zip(system.substances, concentrations))
result

{'H+': 3.4177702795991742e-09,
 'H2O': 55.499997074115974,
 'H3CCOO-': 0.014997077533741783,
 'H3CCOOH': 2.922466258210992e-06,
 'OH-': 2.9258840281057227e-06}

Passando a concentração de H⁺ para a seguinte função, retorna o pH:

def pH(hydronium_concentration):
    return -np.log10(hydronium_concentration)

print(f"{pH(result['H+']):.2f}")

8.47

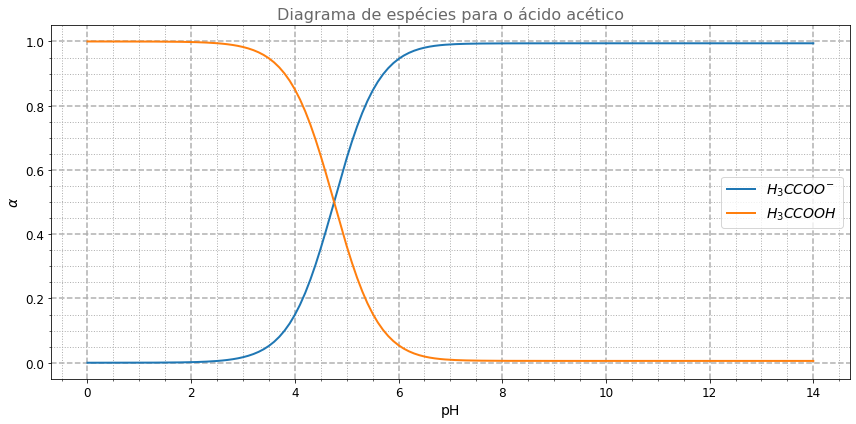
Também podemos obter o diagrama de espécies para o ácido acético. Para isso, precisamos das frações molares do acetato e do ácido acético. Vamos criar uma função que recebe todas as espécies do sistema e retira as espécies que não serão utilizadas, retornando um dicionário das frações molares das espécies de interesse, acetato e ácido acético:

def mole_fractions(substances):
    for key in ('H+', 'OH-', 'H2O'):
        substances.pop(key, None)
    frac = dict()
    total = sum(substances.values())
    for key, value in substances.items():
        frac[key] = value / total
    return frac

Agora vamos criar um dicionário para armazenar as frações molares das espécies de interesse e criar o range de pH. O fractions foi inicialmente criado como uma lista vazia para posteriormente armazenar os valores das frações molares para cada valor de pH.

species = [item for item in system.substance_labels() if item not in ('H+', 'OH-', 'H2O')]
fractions = defaultdict(list, {k: [] for k in species})

pH_range = np.arange(0, 14.1, 0.1)

for value in pH_range:
    condition = defaultdict(float, {'H2O': 55.5, 'H+': 10**-value})
    concentrations, _, _ = system.root(condition)
    result = dict(zip(system.substances, concentrations))
    mf = mole_fractions(result)
    for key, value in zip(fractions.keys(), mf.values()):
        fractions[key].append(value)

Podemos obter o gráfico de diagrama das espécies utilizando a biblioteca Matplotlib. Para isso, vamos criar uma figura, passar os eixos e identificar o gráfico:

fig, ax = plt.subplots()

for compound in fractions:
    ax.plot(pH_range, fractions[compound], 
            label=f'${system.substances[compound].latex_name}$')

ax.set_xlabel('pH')
ax.set_ylabel(r'$\alpha$')
ax.grid(b=True, axis='both', which='major', linestyle='--', linewidth=1.5)
ax.minorticks_on()
ax.grid(b=True, axis='both', which='minor', linestyle=':', linewidth=1.0)
ax.set_axisbelow(True)

ax.legend()
ax.set_title('Diagrama de espécies para o ácido acético', color='dimgray')

plt.show()

Conclusão
#

Nesse artigo, vimos algumas funcionalidades das bibliotecas Molmass, Mendeleev e ChemPy e o quanto essas ferramentas são úteis na resolução de atividades da rotina de estudantes e profissionais da área química. Vimos que podemos agilizar cálculos simples, como de massa molar, até mais complexos como de concentração de espécies e de cinética.

Este artigo é uma colaboração minha, Helena Benevenuto, com o Ciência Programada. Me acompanhe no LinkedIn para mais conteúdos de química.

Compartilhe este artigo em suas redes e siga o projeto Ciência Programada para sempre estar atualizado. Até a próxima.