Resolvendo equações com SymPy

Grande parte do estudo de matemática em níveis mais fundamentais é dedicada a resoluções de equações e sistemas de equações. Neste artigo veremos como utilizar o SymPy para essas tarefas de forma rápida e intuitiva.

A famosa equação de 2° grau

#

Vamos começar importando o SymPy e criando alguns símbolos. Já falamos sobre criação de símbolos no primeiro artigo dessa série sobre SymPy então, se tiver dúvidas, dê uma olhada lá.

import sympy

# configuração para outputs melhores no artigo, pode ser ignorado
sympy.init_printing(use_latex='png', scale=1.0, order='grlex',
                    forecolor='Black', backcolor='White',)

x, y, a, b, c = sympy.symbols('x y a b c')

Usando expressões e solve

#

Vamos agora criar uma expressão na variável x:

expr = x**2 + 2*x - 8

Como podemos ver, a expressão é de grau 2 em x:

expr

\(\displaystyle x^{2} + 2 x - 8\)

Assim, se igualarmos a expressão a zero, teremos uma equação quadrática, a famosa equação de 2° grau, e poderíamos resolver tal equação. Ou seja, achar os valores de x para os quais a equação tem valor zero, as raízes da equação. Para isso, usamos o método solve com a assinatura solve(expr, var), sendo var a variável para a qual se quer resolver a equação:

sympy.solve(expr, x)

\(\displaystyle \left[ -4, \ 2\right]\)

Assim, vemos que as raízes da equação x²+2x-8=0 são -4 e 2.

Agora o grande poder do SymPy é ser um CAS simbólico. Logo, podemos ter as expressões gerais para raízes de uma equação de segundo grau escrita na forma geral ax²+bx+c=0:

sympy.solve( a*x**2 + b*x + c, x)

\(\displaystyle \left[ \frac{- b - \sqrt{- 4 a c + b^{2}}}{2 a}, \ \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}\right]\)

Ora, nada mais é que a famosa fórmula de Bhaskara para resolução de equações de segundo grau. A fórmula geralmente apresentada nos livros contém o símbolo ± para indicar que são duas raízes. Acima temos de forma mais explícita as duas raízes.

Vimos anteriormente que a solução é apresentada na forma de uma lista com cada raiz. Vamos, então, ver cada solução separadamente acessando cada item da lista da forma usual em Python:

solutions = sympy.solve( a*x**2 + b*x + c, x)

solutions[0]

\(\displaystyle \frac{- b - \sqrt{- 4 a c + b^{2}}}{2 a}\)

solutions[1]

\(\displaystyle \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}\)

Por listas serem iteráveis, podemos fazer um loop substituindo a, b e c pelos valores utilizados na primeira expressão desse artigo e verificar que as raízes são, realmente, -4 e 2:

roots = []
for solution in solutions:
    roots.append(solution.subs({'a': 1, 'b': 2, 'c': -8}))
    
roots

\(\displaystyle \left[ -4, \ 2\right]\)

Usando igualdades e solve

#

A abordagem anterior é perfeitamente correta e é muito usada em scripts e tutoriais que você encontra na internet. No entanto, há outra forma de abordar o problema que utiliza uma abstração de igualdade que existe no SymPy e que, particularmente, acho mais interessante por ser mais semântica, mais próxima do que efetivamente queremos representar matematicamente.

O SymPy possui a classe Equality que tem por intuito expressar a igualdade entre dois objetos. Há a abreviação Eq que torna mais fácil de escrever códigos. Assim, a mesma expressão anterior, que traduzimos implicitamente como equação apenas quando fizemos solve(expr, x), poderia ser mais explicitamente ser reconhecida diretamente como equação com:

equation = sympy.Eq(x**2 + 2*x - 8, 0)
equation

\(\displaystyle x^{2} + 2 x - 8 = 0\)

Veja que agora efetivamente escrevemos como uma equação, com um lado esquerdo e um direito. O direito, no caso, sendo o número zero. Certamente essa forma é mais facilmente compreendida.

E, claro, podemos passar essa equação para o solve e obter as mesmas raízes:

sympy.solve(equation, x)

\(\displaystyle \left[ -4, \ 2\right]\)

Não necessariamente o lado direito precisa ser zero. A mesma equação poderia ser representada por:

sympy.Eq(x**2 + 2*x, 8)

\(\displaystyle x^{2} + 2 x = 8\)

Que, obviamente, resultaria nas mesmas raízes ao ser passada para solve:

sympy.solve(sympy.Eq(x**2 + 2*x, 8), x)

\(\displaystyle \left[ -4, \ 2\right]\)

Sistemas de equações

#

Já vimos que podemos resolver uma equação, mas e um sistema? Podemos facilmente. A primeira forma é passando um iterável de expressões para solve e, também, as variáveis do sistema. Suponha um sistema formado pelas equações x + y = 3 e 3x - 2y = 0. Poderíamos escrever:

sympy.solve((x + y - 3, 3*x - 2*y), 
            (x, y))

\(\displaystyle \left\{ x : \frac{6}{5}, \ y : \frac{9}{5}\right\}\)

Poderíamos, também, ser mais explícitos criando cada equação com Eq e passando para solve:

eq1 = sympy.Eq(x + y, 3)
eq2 = sympy.Eq(3*x - 2*y, 0)

sympy.solve((eq1, eq2), 
            (x, y))

\(\displaystyle \left\{ x : \frac{6}{5}, \ y : \frac{9}{5}\right\}\)

Cuidado com floats!

#

Observe que o resultado do sistema saiu na forma de um dicionário. E podemos efetivamente substituir em qualquer equação para ver o resultado:

eq1.subs({x: 6/5, y: 9/5})

\(\displaystyle \text{True}\)

O que significa o resultado True? Significa que a igualdade da equação e satisfeita. Veja a representação de eq1:

eq1

\(\displaystyle x + y = 3\)

Assim, o True significa que, quando os valores passados substituem x e y na equação, a igualdade é satisfeita, é verdadeira.

Bom, seria de se esperar que a mesma substituição em eq2 retornaria True, certo?

eq2.subs({x: 6/5, y: 9/5})

\(\displaystyle \text{False}\)

Ué…?!

Cuidado com floats! No primeiro artigo sobre SymPy já abordamos um pouco disso e vimos como podemos representar frações no SymPy. Veja, quando se escreve 6/5 em Python o que temos é:

6/5

\(\displaystyle 1.2\)

Ou seja, um float. E operações com floats envolvem aproximações, como vimos no artigo já citado. Assim, compensa transformar em representações de frações do SymPy:

eq2.subs({x: sympy.S('6/5'), y: sympy.S('9/5')})

\(\displaystyle \text{True}\)

Agora sim, temos a igualdade como válida.

Completando quadrados

#

Completar quadrados é uma técnica para converter um polinômio na forma ax²+bx+c para a forma a(x-h)²+k para alguns valores de h e k. É utilizada em diversos contextos de ensino, sendo o mais conhecido na derivação da fórmula quadrática de Bhaskara.

Na animação a seguir, vemos que h=-b ⁄ (2a) e k= c-(b² ⁄ 4a):

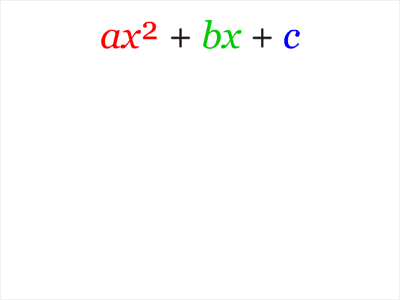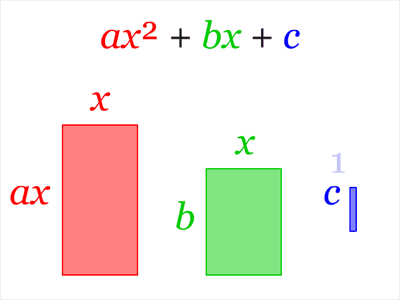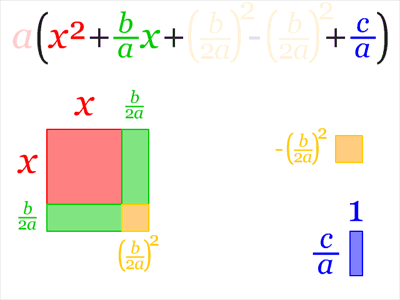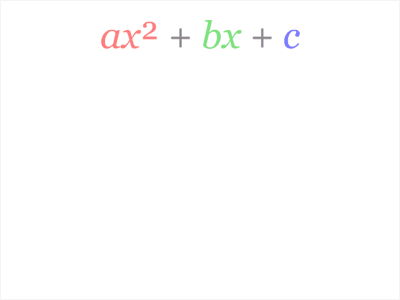
Precisamos, então, criar dois novos símbolos:

h, k = sympy.symbols('h k')

Podemos, apenas como recurso didático, expressar a igualdade pelo SymPy:

square = sympy.Eq(a * x**2 + b*x + c, a * (x - h)**2 + k)
square

\(\displaystyle a x^{2} + b x + c = a \left(- h + x\right)^{2} + k\)

Vamos, agora, pegar uma equação quadrática qualquer e tentar achar os valores de h e k. Por exemplo: x²-4x+7 = (x-h)²+k

square_example = sympy.Eq(x**2 - 4*x + 7, (x - h)**2 + k)
sympy.solve(square_example, (h, k))

\(\displaystyle \left\{ h : 2, \ k : 3\right\}\)

Conhecendo mais o objeto Equality

#

Vamos aproveitar e conhecer melhor o objeto Equality com esse exemplo. Até o momento, o utilizamos como uma forma de representar uma equação matemática, mas já vimos que o retorno pode ser também um booleano, True ou False. Vamos entender.

Primeiro, vamos substituir os valores encontrados para h e para k em nosso objeto:

square_example.subs({h: 2, k: 3})

\(\displaystyle x^{2} - 4 x + 7 = \left(x - 2\right)^{2} + 3\)

É possível obter cada lado da igualdade com os atributos rhs (lado direito, right hand side) e lhs (lado esquerdo, left hand side):

square_example.subs({h: 2, k: 3}).rhs

\(\displaystyle \left(x - 2\right)^{2} + 3\)

square_example.subs({h: 2, k: 3}).lhs

\(\displaystyle x^{2} - 4 x + 7\)

Podemos expandir o quadrado do lado direito:

square_example.subs({h: 2, k: 3}).rhs.expand()

\(\displaystyle x^{2} - 4 x + 7\)

Bom, isso mostra que efetivamente os dois lados são iguais, certo? Logo, a seguinte comparação de igualdade deve ser verdadeira:

square_example.subs({h: 2, k: 3}).lhs == square_example.subs({h: 2, k: 3}).rhs

False

Só que não… por que? Conforme a documentação do SymPy, a biblioteca analisa igualdade de forma e não equivalência matemática. Para detalhes, veja esta parte da documentação do SymPy e esse FAQ no repositório do SymPy.

Pelo que foi visto, se a comparação for entre o lado esquerdo e a expansão do lado direito, o resultado deve ser True:

square_example.subs({h: 2, k: 3}).lhs == square_example.subs({h: 2, k: 3}).rhs.expand()

True

Agora sim. E tudo poderia ser resumido na linha seguinte, que instrui o SymPy a fazer as expansões possíveis e verificar a igualdade:

square_example.subs({h: 2, k: 3}).expand()

\(\displaystyle \text{True}\)

Conclusão e mais artigos sobre SymPy

#

A tentação de fazer toda e qualquer equação que apareça na sua frente com o SymPy agora deve ser grande. Sistemas então, nem se fala! Mas veja como é importante ter um bom fundamento matemático para entender o que se pode fazer com a biblioteca. Não saia matando aula de matemática (ou até mate, mas depois estude pelos livros ;-) ).

Até a próxima.