Muitos consideram matemática, física e afins matérias difíceis, geralmente pela abordagem tradicional vista nas escolas. Mas a verdade é que, mostradas de uma forma mais adequada, são áreas sensacionais e que, se dominadas, nos ajudam a dar outra visão de mundo. E computadores podem ajudar em etapas mais complexas e tediosas das manipulações aritméticas. Nesse artigo, começaremos a explorar a biblioteca SymPy, aproveitando para fazer uma boa revisão de conceitos matemáticos fundamentais.
Introdução e instalação do SymPy #
Um sistema algébrico computacional (em inglês computer algebra system (CAS)) pode ser utilizado para cálculos com expressões matemáticas complicadas, resolução de equações, simulações, dentre outras aplicações.
Há sistemas gratuitos como o SymPy e o Octave, e comerciais como Maple, MATLAB e Mathematica. Em essência, todos oferecem as mesmas funcionalidades, de forma que a escolha recai em decidir aspectos técnicos e de custo X benefício, especialmente no que diz respeito a integrações com outras ferramentas. Nesse sentido, o SymPy tem uma grande vantagem, já que a linguagem Python é largamente utilizada em diversos contextos de forma que facilmente se pode expandir as funcionalidades. Inclusive, no site do projeto SymPy, estes são os pontos destacados:
- gratuito, sob a licença BSD
- baseado em Python
- leve, tendo como única dependência a biblioteca
mpmath - é uma biblioteca, podendo ser usada em outras aplicações e extendida facilmente
E, o principal motivo para a escolha do SymPy, você pode conferir suas respostas para as listas de cálculo da faculdade ou daquelas provas de professores sem criatividade, com um monte de conta e sem nenhuma aplicação real ou contextualização ;-) Só não diga que eu escrevi isso.

E se você é professor e a carapuça serviu, calma e respira. É óbvio que o aluno precisa aprender cálculo, até porque se não souber o mínimo não vai nem ao menos saber usar o pacote, computadores não fazem milagres, devolvem exatamente o que foi solicitado. A crítica é sobre aplicar esses conhecimentos em casos reais. Crie projetos onde as contas são aplicadas, crie resolvedores de problemas e não calculadoras humanas.
O SymPy é um sistema algébrico computacional simbólico. Isto significa que números e operações são representados simbolicamente permitindo obter resultados exatos. Vamos entender isso melhor.
Considere o número \(\sqrt{2}\). No SymPy, tal número é representado pelo objeto
Pow(2, 1/2), enquanto que em CAS numéricos, como o Octave, é representado como
uma aproximação 1.41421356237310 (um float). Mas e daí? Bom, dependendo da
aplicação, não há problemas em haver essa aproximação, mas ela pode levar a
problemas. Vamos ver um exemplo.
Se usarmos o método sqrt do pacote math do Python, também teremos a raiz
armazenada como um float:
import math
math.sqrt(2)
1.4142135623730951
Ora, sabemos que se elevar \(\sqrt{2}\) ao quadrado, devemos ter o número 2, correto? Vejamos:
math.sqrt(2)**2
2.0000000000000004
Viu o que aconteceu? Há um “4” perdido ali que, de forma bem simplificada, surge do fato de a representação ser uma aproximação.
E qual a consequência disso? Poderíamos listar algumas, mas vou focar em uma que
pega muitos iniciantes de surpresa. É muito comum o uso de comparações com ==
em condicionais ou em testes de funções. Essas comparações correm sério risco de
falhar quando envolvem floats:
math.sqrt(2)**2 == 2
False
O que fazer nesses casos? Bom, se o contexto exigir continuar utilizando aproximações numéricas e floats, uma forma simples, mas nem sempre confiável, é comparar com uma tolerância aceitável no contexto. Por exemplo, digamos que um erro de 1 em 10000 é aceitável em um dado contexto. Assim, o teste poderia ser escrito como:
math.sqrt(2)**2 - 2 < 1E-4
True
Em algum momento vou fazer artigos abordando melhor os cuidados a se tomar quando trabalhar com floats, mas no momento fica essa recomendação de leitura: aritmética com floats da própria documentação do Python.
Vejamos como se comporta o SymPy nesse exemplo simples.
Primeiro, a instalação pode ser feita com um simples pip install sympy. Caso
utilize o Anaconda, que já escrevemos sobre
aqui,
o SymPy já está instalado. A importação é simples:
import sympy
Vamos ver como é a representação da raiz quadrada de 2:
sympy.sqrt(2)
\(\displaystyle \sqrt{2}\)
Observe que apareceu o símbolo \(\sqrt{2}\) e não uma aproximação na forma de float. Vamos fazer a operação de elevar ao quadrado:
sympy.sqrt(2)**2
\(\displaystyle 2\)
Obtivemos o resultado exato 2. Inclusive podemos verificar que é realmente o número 2 com a comparação:
sympy.sqrt(2)**2 == 2
True
E, sendo a expressão tratada simbolicamente, pode ser simplificada simbolicamente. Lembra que \(\sqrt{8} = 2\sqrt{2}\)? Então:
sympy.sqrt(8)
\(\displaystyle 2 \sqrt{2}\)
O SymPy cuidou dessa simplificação para você. E, mais, simbolicamente fica explícita essa relação, enquanto que se você fizer \(\sqrt{8}\) na sua calculadora ou usando um pacote numérico dificilmente perceberá que o resultado corresponde a \(2\sqrt{2}\):
math.sqrt(8)
2.8284271247461903
Vamos agora ver o básico de matemática com SymPy.
Matemática básica com SymPy #
Vamos entender como o SymPy representa objetos matemáticos e operações simples. Mas antes, vamos nos lembrar que em Python há dois tipos numéricos principais: inteiros e floats.
3 # int
3
3.0 # float
3.0
Floats são representações aproximadas de números reais, até a 16ª casa decimal. Quando fazemos uma divisão, mesmo que de inteiros, o resultado é um float:
1/1
1.0
1/7
0.14285714285714285
A chamada divisão inteira, representada por duas barras, fornece a parte inteira da divisão:
1//7
0
Enquanto que o sinal %, conhecido como módulo, fornece o resto da divisão:
1 % 7
1
Números racionais #
Agora, sabemos que 1/7 pertence ao conjunto dos números racionais e sua
representação decimal é infinitamente longa. Para uma representação exata,
precisamos do método sympify do SymPy:
sympy.sympify('1/7')
\(\displaystyle \frac{1}{7}\)
Que pode ser chamado abreviadamente de S:
sympy.S('1/7')
\(\displaystyle \frac{1}{7}\)
Veja como foi passada a fração para o método, como uma string. Vamos ver o tipo do objeto gerado:
type(sympy.S('1/7'))
sympy.core.numbers.Rational
Logo, a mesma fração poderia ser criada como:
sympy.Rational(1, 7)
\(\displaystyle \frac{1}{7}\)
Observe que na forma acima passados o numerador e o denominador na forma de inteiros. Podemos fazer operações entre racionais:
sympy.Rational(1, 2) + sympy.S('1/3')
\(\displaystyle \frac{5}{6}\)
Um objeto SymPy dividido por um inteiro resulta em um objeto SymPy:
sympy.S('1')/7
\(\displaystyle \frac{1}{7}\)
Obtendo aproximações numéricas #
Durante a resolução de problemas, é melhor deixar para obter a representação
numérica apenas ao final. Para obter a aproximação numérica de um objeto SymPy
como um float, usamos o método evalf(). Vamos ver um exemplo com o número
\(\pi\):
sympy.pi
\(\displaystyle \pi\)
type(sympy.pi)
sympy.core.numbers.Pi
Observe que é um tipo específico do SymPy, que possui alguns números em sua biblioteca. Veremos alguns no decorrer do tempo. Vejamos a representação como float:
sympy.pi.evalf()
\(\displaystyle 3.14159265358979\)
type(sympy.pi.evalf())
sympy.core.numbers.Float
Observe acima que o SymPy possui uma classe Float própria (o mesmo vale para
inteiros e outros tipos de números), não utilizando o float padrão do Python.
Assim, cuidado ao misturar tipos padrão do Python e tipos SymPy. Na dúvida,
aplique o método sympify já mostrado para garantir que tudo está como objetos
SymPy.
Uma forma resumida de chamar o método evalf é simplesmente usar o método n:
sympy.pi.n()
\(\displaystyle 3.14159265358979\)
É possível solicitar mais casas decimais. Por exemplo, se desejarmos 50 casas decimais para o número \(\pi\):
sympy.pi.n(50)
\(\displaystyle 3.1415926535897932384626433832795028841971693993751\)
Isso é possível pois o SymPy utiliza a biblioteca mpmath por baixo, que permite cálculos com precisão aritmética arbitrária.
Também existe uma função global N para obter uma representação numérica de
objetos SymPy:
sympy.N(sympy.pi)
\(\displaystyle 3.14159265358979\)
Como é matemática simbólica, podemos utilizar, por exemplo, a noção de infinito,
que possui o curioso símbolo oo:
sympy.oo
\(\displaystyle \infty\)
sympy.oo > 100
\(\displaystyle \text{True}\)
Símbolos #
Como estamos falando de álgebra simbólica, nada melhor que vermos como criar
símbolos com SymPy. De Python, sabemos que, se utilizarmos algum símbolo não
definido previamente, um NameError será levantado:
x + 2
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
/tmp/ipykernel_342/917526016.py in <module>
----> 1 x + 2
NameError: name 'x' is not defined
A partir do momento que definirmos x, ele pode ser utilizado. E, em Python,
não há necessidade de declarar o tipo de x:
x = 2
x + 2
4
A questão é que gostaríamos que x fosse reconhecido como um símbolo. Pense no
x das aulas de matemática do ensino fundamental, das famosas questões de
“encontre o x”:
Hehe…
Ou seja, queremos x com o sentido clássico de uma variável matemática. Podemos
fazer da seguinte forma:
x = sympy.Symbol('x')
x + 2
\(\displaystyle x + 2\)
Veja que agora aparece como uma expressão matemática. Podemos criar vários
símbolos ao mesmo tempo, repare que agora o método é symbols:
y, z = sympy.symbols('y z')
x + y + z - 5
\(\displaystyle x + y + z - 5\)
O SymPy permite criar símbolos que sigam um padrão. Por exemplo, no estudo de
polinômios é muito comum representar todos os coeficientes com a letra a
mudando apenas o número subscrito. Isso pode ser criado com uma representação
muito similar à representação de slices de sequências em Python, na qual o
último número é excluso:
a1, a2, a3, a4 = sympy.symbols('a1:5')
a4 * x**4 + a3 * x**3 + a2 * x**2 + a1 * x + 2
\(\displaystyle a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + 2\)
Veja que por padrão o SymPy apresenta o polinômio do menor grau em x para o
maior, deixando o termo de \(x^0\) para o final. É possível mudar a ordem
alterando a instrução de ordem
monomial do método
init_printing, que configura como serão apresentadas as expressões do SymPy.
Vejamos:
sympy.init_printing(order='grlex')
a4 * x**4 + a3 * x**3 + a2 * x**2 + a1 * x + 2
\(\displaystyle a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + 2\)
grlex vem de graded lexicographic
order,
partindo do maior grau para o menor, o que é mais usual em textos matemáticos e
afins. Para voltar ao padrão do SymPy, usamos a opção lex:
sympy.init_printing(order='lex')
a4 * x**4 + a3 * x**3 + a2 * x**2 + a1 * x + 2
\(\displaystyle a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + 2\)
De acordo com a documentação do
SymPy, algumas letras são
reservadas e deve se evitar utilizá-las como símbolos: I, E, N, S, O,
Q e C. N e S já vimos anteriormente. I e E representam o número
imaginário \(i \equiv \sqrt{-1}\) e a base do logaritmo natural, respectivamente:
sympy.I
\(\displaystyle i\)
sympy.E
\(\displaystyle e\)
O O é utilizado para notação de big
O:
sympy.O
sympy.series.order.Order
sympy.O(x**2) * x
\(\displaystyle O\left(x^{3}\right)\)
O C e o Q têm usos mais específicos, que fogem ao escopo desse material
introdutório, mas que podem ser vistas na documentação já citada.
Expressões #
Expressões podem ser criadas combinando símbolos com operações matemáticas e outras funções:
expr = 2 * x + 3 * x - sympy.sin(x) - 3 * x + 42
expr
\(\displaystyle 2 x - \sin{\left(x \right)} + 42\)
Observe que a expressão já foi apresentada simplificada, pois se trata de um caso simples de adição. Em casos mais elaborados, o SymPy não é proativo na simplificação, tendo em vista que pode ser de interesse do usuário obter a expressão crua, sem manipulações. Mas é possível solicitar a simplificação.
Simplificando expressões e obtendo coeficientes #
Há um método específico para simplificação:
(x + x * y) / x
\(\displaystyle \frac{x y + x}{x}\)
sympy.simplify(_)
\(\displaystyle y + 1\)
O underscore _ pega o resultado da célula anterior e passa para o simplify.
Voltando para nossa expressão expr, é possível verificar os coeficientes dos
termos em x com o método coeff, supondo a expressão como um polinômio em
x:
expr.coeff(x)
\(\displaystyle 2\)
Como a expressão é de ordem 1 em x, não há, por exemplo, coeficiente para um
termo de ordem 2 ou, melhor dizendo, tal coeficiente é zero:
expr.coeff(x, 2)
\(\displaystyle 0\)
Se quisermos a parcela 42 na expressão, basta solicitar o coeficiente do termo
x^0:
expr.coeff(x, 0)
\(\displaystyle 42\)
É possível também verificar os coeficientes relativos a outros termos, basta tratá-los como se fossem a variável do polinômio:
expr.coeff(sympy.sin(x))
\(\displaystyle -1\)
Fatoração e expansão (distributiva) #
Há métodos para diversas operações matemáticas usuais em expressões. Por exemplo, a operação de fatoração:
sympy.factor(x**2 - 2*x - 8)
\(\displaystyle \left(x - 4\right) \left(x + 2\right)\)
E a contrária, a expansão ou multiplicação distributiva:
sympy.expand( (x - 4)*(x + 2) )
\(\displaystyle x^{2} - 2 x - 8\)
Também é possível fazer expansões de expressões trigonométricas. Por exemplo:
sympy.cos(x + y)
\(\displaystyle \cos{\left(x + y \right)}\)
sympy.expand(_, trig=True)
\(\displaystyle - \sin{\left(x \right)} \sin{\left(y \right)} + \cos{\left(x \right)} \cos{\left(y \right)}\)
O método collect #
Quando símbolos são utilizados como coeficientes, o SymPy não os junta. Mas
podemos usar o método collect que coleta aditivamente termos com relação a uma
potência. Para entender, vamos criar dois símbolos, a e b, e criar uma
expressão com os mesmos:
a, b = sympy.symbols('a b')
expr = x**2 + x*b + a*x + a*b
expr
\(\displaystyle a b + a x + b x + x^{2}\)
Vamos, então, passar a expressão para o método collect, dizendo para agrupar
os coeficientes do termo x^1:
sympy.collect( expr, x )
\(\displaystyle a b + x^{2} + x \left(a + b\right)\)
Observe que a expressão foi escrita de forma a deixar explícito que o
coeficiente do termo x é (a + b). Isso pode ser útil em alguns contextos,
especialmente para apresentação.
No entanto, mesmo sem escrever explicitamente, o SymPy já reconhece internamente
o coeficiente como (a + b), como se pode ver com o método coeff:
expr.coeff(x, 1)
\(\displaystyle a + b\)
Substituindo valores em uma expressão #
Algo de muito interesse no contexto de expressões matemáticas é poder substituir valores para verificar qual o valor da expressão após tal substituição. Vamos criar uma nova expressão:
expr = sympy.sin(x) + sympy.cos(y)
expr
\(\displaystyle \sin{\left(x \right)} + \cos{\left(y \right)}\)
Com o método subs, podemos passar um dicionário com os valores desejados para
cada símbolo:
expr.subs({x: 1, y:2})
\(\displaystyle \cos{\left(2 \right)} + \sin{\left(1 \right)}\)
Observe que o retorno foi ainda simbólico, mas podemos ver uma aproximação em
float usando o método n visto anteriormente:
expr.subs({x: 1, y:2}).n()
\(\displaystyle 0.425324148260754\)
Caso o resultado da substituição seja exato, o retorno será apresentado diretamente. Por exemplo, sabemos que \(\sin(\pi) = 0\) e \(\cos(0) = 1\). De forma que a soma daria 1. Vejamos:
expr.subs({x: sympy.pi, y:0})
\(\displaystyle 1\)
O mesmo para outros ângulos notáveis, que possuem representações simbólicas. Por exemplo:
expr.subs({x: sympy.pi/2, y:sympy.pi/4})
\(\displaystyle \frac{\sqrt{2}}{2} + 1\)
Caso não tenha entendido, relembre os ângulos notáveis com a imagem seguinte do círculo unitário:
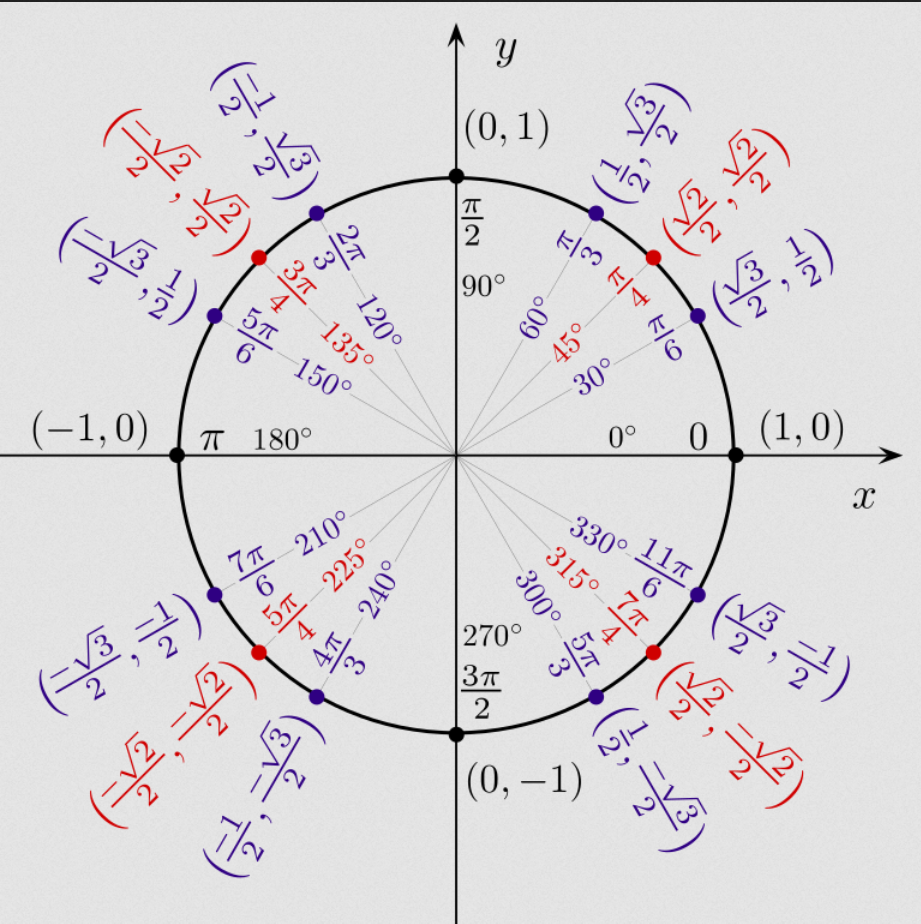
No caso de se solicitar uma substituição com valores já aproximados, teremos o seguinte tipo de resultado:
expr.subs({x: sympy.pi/2.5, y:sympy.pi/4.3})
\(\displaystyle \cos{\left(0.232558139534884 \pi \right)} + \sin{\left(0.4 \pi \right)}\)
Conclusão e mais artigos sobre SymPy #
Neste artigo vimos o básico de SymPy e espero que tenha sido possível perceber o poder dessa biblioteca. Esse é apenas o primeiro de uma série de artigos sobre a biblioteca.
Até a próxima.

